The NP-hard problems are solved in polynomial time by non-deterministic machines and are difficult to find but simple to prove. NP (Nondeterministic Polynomial) is a class of decision problems in computer science where a proposed solution can be verified quickly. NP-hard problems are at least as challenging as the hardest problems in NP, and solving them efficiently is believed to be extremely difficult, though not necessarily impossible.
What is an NP Problem?
If a problem is in NP and is equally difficult as any other problem in NP, it belongs to the class NPC. Even if a problem is not in NP itself, it is NP-hard if all problems in NP can be reduced to it in polynomial time.
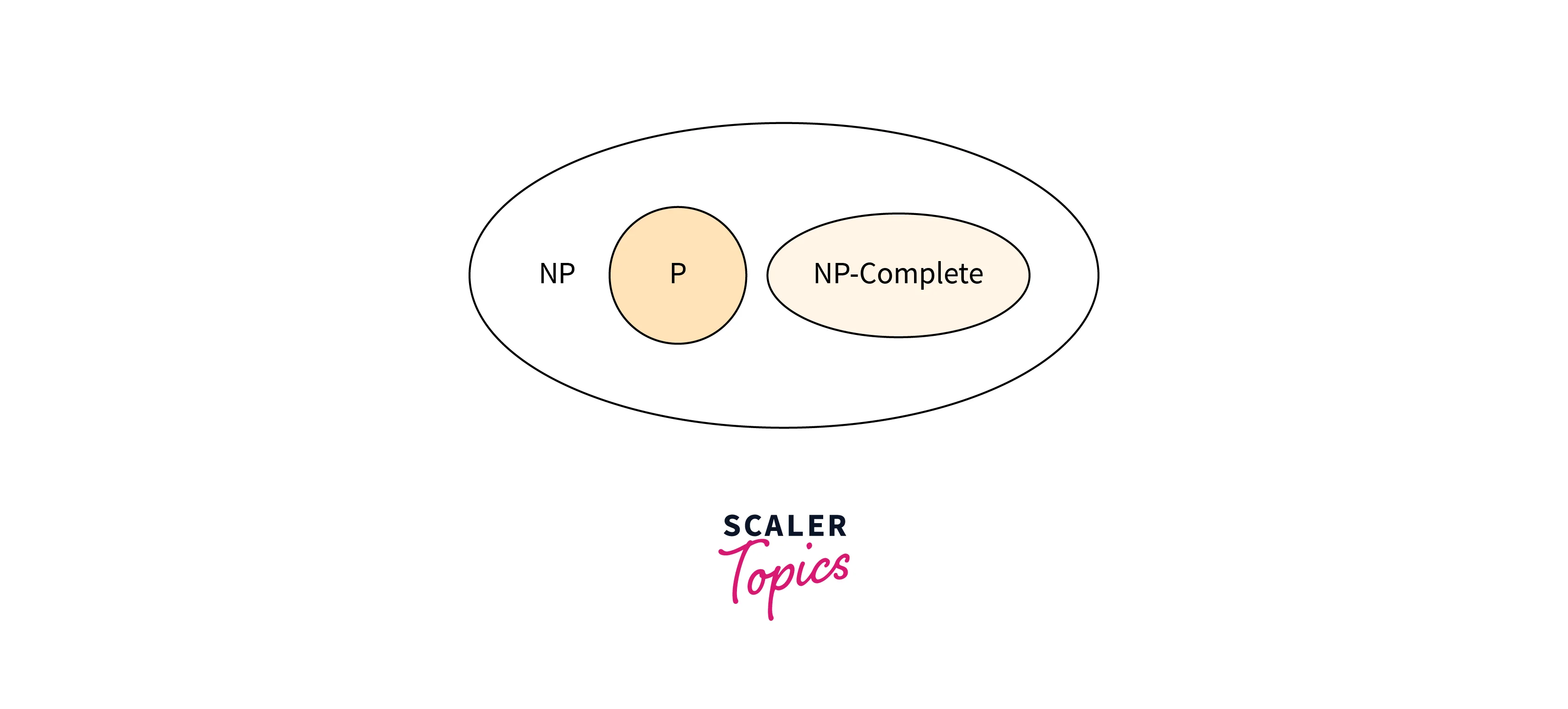
All NP problems would be solvable in polynomial time if a polynomial time algorithm existed for one of these issues. These issues are referred to as NP-complete. NP-completeness is a phenomenon that is significant for both theoretical and practical reasons.
If a language B meets both of these requirements, it is NP-complete.
B is in NP
Every A in NP is polynomial time reducible to B.
Language B is called NP-Hard if it meets the second property but not necessarily the first. If there is an NP-Complete problem A that Turing reduces to B, then a search problem B is NP-Hard.
Until P = NP, the NP-Hard issue cannot be solved in polynomial time. Looking for an effective algorithm is unnecessary when a problem is revealed to be NPC. We can instead concentrate on creating an approximation algorithm.
NP-Hard Problem
If problem Y is NP-Complete and convertible to X in polynomial time, then issue X is NP-Hard. The difficulty of NP-Hard and NP-Complete tasks is equal. NP class is not required for NP-Hard Problems.
If every NP problem can be solved in a polynomial amount of time, it is called NP-Hard.
Examples
The following problems are NP-Hard:
- The circuit-satisfiability problem
- Set Cover
- Vertex Cover
- Travelling Salesman Problem
NP Complete Problem
If a problem Y exists and is reducible to X in polynomial time, then the problem X is NP-Complete. Both NP and NP-Complete problems are challenging. If a problem is a NP and NP-Hard Problems component, it is NP-Complete. In polynomial time, a non-deterministic Turing machine can solve an NP-Complete problem.
When an issue is np-complete, it is np and np hard together.
np complete issues can, therefore, be verified in polynomial time, according to this.
Examples
Following are some NP-Complete problems, for which no polynomial time algorithm is known.
- Determining whether a graph has a Hamiltonian cycle
- Determining whether a Boolean formula is satisfiable, etc
Difference between NP Hard and NP Complete
| Characteristic | NP-Hard | NP-Complete |
|---|---|---|
| Solvability | Can be solved if and only if reducible to | Can be solved by non-deterministic algorithm |
| Time Complexity | Time complexity unknown | Polynomial time complexity |
| Membership in NP | Not required | Must belong to NP and NP-hard |
| Nature of Problems | Not exclusive to decision problems | Exclusively decision problems |
| Relationship Between Categories | Not all NP-hard problems are NP-complete | All NP-complete problems are NP-hard |
| Decision vs. Optimization Problems | May involve optimization problems | Exclusively involves decision problems |
| Examples | Halting problem, Vertex cover problem, etc. | Determine whether a graph has a Hamiltonian cycle, Determine whether a Boolean formula is satisfiable or not, Circuit-satisfiability problem, etc. |
| Completeness under Polynomial-Time Reduction | NP-complete problems are polynomial-time reducible to one another. | NP-hard problems are not necessarily polynomial-time reducible to each other. |
| Existence of Efficient Verification | NP-complete problems have efficient algorithms to verify proposed solutions in polynomial time. | For NP-hard problems, there is no known efficient algorithm to verify a proposed solution. |
FAQs
Q1: What does “NP” stand for in NP-hard and NP-complete problems?
A1: “NP” stands for “Nondeterministic Polynomial.” It’s a complexity class in computer science that represents problems for which a proposed solution can be verified quickly.
Q2: What is the main difference between NP-hard and NP-complete problems?
A2: NP-hard problems are decision problems that are at least as hard as the hardest problems in NP but may not be in NP themselves. NP-complete problems, on the other hand, are both in NP and NP-hard.
Q3: Can NP-hard problems be solved efficiently?
A3: Solving NP-hard problems efficiently is generally believed to be difficult, and no polynomial-time algorithms are known for them. However, they can sometimes be approximated or solved in suboptimal ways.
Q4: How can I recognize if a problem is NP-hard or NP-complete?
A4: Identifying whether a problem is NP-hard or NP-complete often requires demonstrating that it is at least as hard as a known NP-complete problem through a polynomial-time reduction.
Conclusion
- NP-Hard problems are a class of decision problems that are at least as hard as the hardest problems in NP (nondeterministic polynomial time), but they may not be in NP themselves. Solving them exactly often requires exponential time.
- NP-Complete problems, a subset of NP-Hard problems, have the unique property that they are both in NP and NP-Hard. They are some of the most challenging problems in computer science because if you can find a polynomial-time algorithm to solve one of them, you can solve all problems in NP efficiently.
- The concept of NP-Hard and NP-Complete problems is vital in understanding computational complexity theory, as it helps classify problems based on their difficulty and solvability.
- Many real-world problems, such as the Traveling Salesman Problem and the Knapsack Problem, are NP-Hard or NP-Complete. This complexity classification is used to identify whether approximate solutions or heuristics are more suitable in practice.
- Researchers have made significant contributions in designing approximation algorithms and heuristics to tackle NP-Hard and NP-Complete problems efficiently, even though exact solutions may be computationally infeasible for large instances.
- The study of NP-Hard and NP-Complete problems plays a central role in cryptography, optimization, and algorithm design, as it helps determine the limits of what can be efficiently computed and secured in the digital world.