Polish Notation

In this article, we will study polish notation in the data structure. Polish Notation in the data structure is a method of expressing mathematical, logical, and algebraic equations universally. This notation is used by the compiler to evaluate mathematical equations based on their order of operations. When parsing mathematical expressions, three types of notations are commonly used : Infix Notation, Prefix Notation, and Postfix Notation.

Scope

In this article, we are going to discuss the points given below :

• In this article, we will go over Polish Notation in a data structure in depth.
• What are the types of polish notation ?
• Converting an Infix Expression to a Postfix Expression.
• Reverse Polish Notation.
• Applications of Polish Notation in the data structure.

Takeaways

Polish Notation in the data structure is a method of expressing mathematical, logical, and algebraic equations universally.

Introduction to Polish Notation in Data Structure

This type of notation was introduced by the Polish mathematician Lukasiewicz. Polish Notation in data structure tells us about different ways to write an arithmetic expression. An arithmetic expression contains 2 things, i.e., operands and operators. Operands are either numbers or variables that can be replaced by numbers to evaluate the expressions. Operators are symbols symbolizing the operation to be performed between operands present in the expression. Like the expression $(1+2) * (3+4)$ standard becomes $* +12 +34$ in Polish Notation. Polish notation is also called prefix notation. It means that operations are written before the operands. The operators are placed left for every pair of operands. Let’s say for the expression a+b, the prefix notation would be +ab.

Types of Notations

Three types of polish notations exist in the data structure. Let’s have look at them one-by-one.

• Infix Notation :
  This polish notation in data structure states that the operator is written in between the operands. It is the most common type of notation we generally use to represent expressions. It’s the fully parenthesized notation. We find it much easier to write mathematical expressions in Infix Notation, but it is difficult to parse expressions on computers in the form of infix Polish Notation.

  (3+7)
  (1*(2+3))

• Prefix Notation :
  This polish notation in data structure states that the operator should be present as a prefix or before the operands. This notation is also known as “Polish Notation”. For example, if we have an expression like x+y, then here x and y are operands, and ‘+’ is the operator. The prefix notation or polish notation of this expression will be "+xy".

  3+7 will convert into +37
  1*(2+3) will convert into *1(+23)

• Postfix Notation :
  This notation states that the operator should be present as a suffix, postfix, or after the operands. It is also known as Suffix notation or Reverse Polish Notation. For example, if we have an expression like x+y, then here x and y are operands, and ‘+’ is the operator. The prefix notation or polish notation of this expression will be "xy+". In general, a computer can easily understand postfix expressions. This notation is universally accepted and is preferred for designing and programming the arithmetic and logical units of a CPU (Central Processing Unit). All the expressions that are entered into a computer are converted into Postfix or Reverse Polish Notation, stored in a stack, and then computed. Therefore, postfix expression plays a vital role in the tech industry.

  3+7  will convert into  37+
  1*(2+3) will convert into (23+)1*

Conversion of an Infix Expression to Postfix Expression

Generally, humans find infix polish notation much easier to understand than postfix or reverse polish notation. To convert each expression from infix to postfix, we assign priority to each of the operators present in the expression. Each operator has its priority for an expression. For example, if we take some operators, i.e., +, -, *, /, then these will be arranged in priority.

Higher Priority Operators : *, /, %.

Lower Priority Operators : +, -.

Order of Operators : +, −, ∗, /, ^.

A Conversion Algorithm for INFIX POLISH NOTATION to POSTFIX POLISH NOTATION is given below :

• Push “(“ in the stack and add “)” at the end of the infix polish notation of the given expression.
• Repeat the below steps for each of the elements present in the Infix Polish Notation.
• If "(" is encountered, then push the element onto the stack.
• If an operand, i.e. a variable or a number, is encountered, we add it in the postfix or reverse polish notation.
• If ")" is encountered, we pop from the stack until the popped element is "(" and add these elements to the postfix expression. After that discard "(" from the stack and do not add it again to the postfix expression.
• If an operator "x" is encountered, then, again and again, pop from the stack and add each operator to the postfix expression which has the same or higher precedence than operator "x".
• After performing step 2 on each element, we will pop all the elements from the stack and add them to the postfix expression.

Let’s see the above points with a dry run :

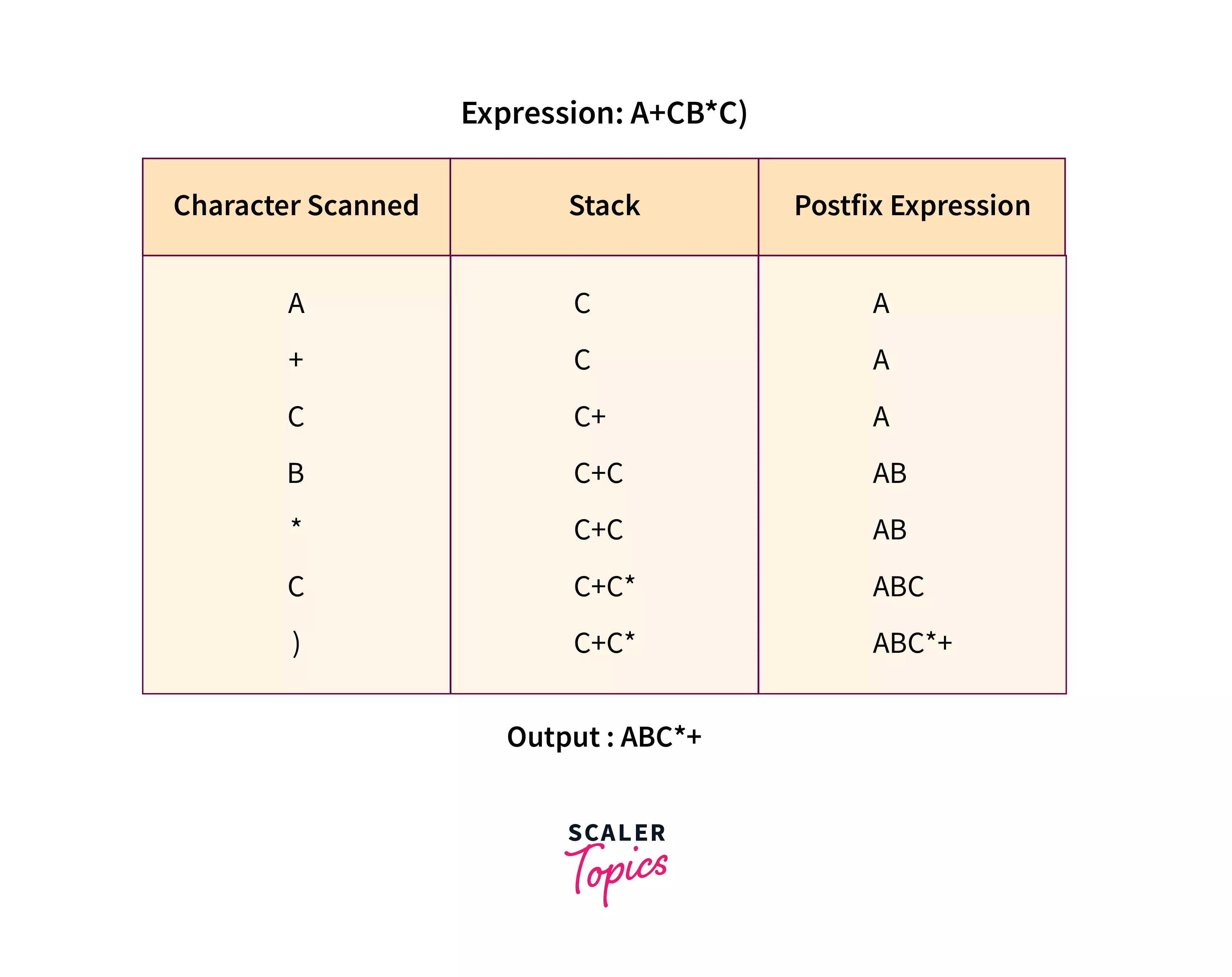
Reverse Polish Notation

Reverse Polish notation is also known as Postfix notation and Suffix Notation. It plays a vital role in the tech industry. In general, humans find Infix polish notation or parenthesized format of expression easy to evaluate, whereas computers find it difficult to parse expressions in the form of Infix Polish Notation, so our computer converts the expression into postfix polish notation or reverse polish notation to evaluate the expression.

A reverse Polish notation states that the operator should be present after the operands. For example, if an expression is x+y, then x and y are operands and ‘+’ is the operator. The prefix notation or polish notation of this expression will be “xy+”.

Sample Code to Evaluate a Postfix notation through stack :

def postfix_eval(postfix_expression):
    postfix_expression = postfix_expression.split()
    n = len(postfix_expression)
    stack = []
    for i in range(n):
        if postfix_expression[i].isdigit():
            stack.append(int(postfix_expression[i]))
        elif postfix_expression[i] == "+":
            x = stack.pop()
            y = stack.pop()
            stack.append(int(x) + int(y))
        elif postfix_expression[i] == "*":
            x = stack.pop()
            y = stack.pop()
            stack.append(int(x) * int(y))
        elif postfix_expression[i] == "/":
            x = stack.pop()
            y = stack.pop()
            stack.append(int(y) / int(x))
        elif postfix_expression[i] == "-":
            x = stack.pop()
            y = stack.pop()
            stack.append(int(y) - int(x))
    return stack.pop()


postfix_expression = "1 2 + 3 *"
ans = postfix_eval(postfix_expression)
print("Infix Expression: ")
print(postfix_expression)
print("Evaluation of Postfix Expression using Stack: ")
print(ans)

Output :

Infix Expression:-
1 2 + 3 *
Evaluation of Postfix Expression using Stack :-
9

This is how we can evaluate a reverse polish notation or postfix expression using Stack.

Applications of Polish Notation

Polish Notation in data structure plays a vital role in the tech industry.

Let’s see some of the applications of the polish notation :

• The Polish Notations play a very vital role in evaluating arithmetic expressions for computers and different types of machines, as they find infix or parenthesized expressions difficult to parse, whereas they find them easy to parse the postfix or reverse polish notation expressions.
• The modern Stack-organized computers are better suited for postfix and prefix notations than normally used infix notations due to their difficulty in parsing.
• The compiler can quickly evaluate these expressions without having to scan the expression for operators first and then for operands, which would require several scans. The compiler can then evaluate the expression in one step by converting the Infix expression to Polish notation.

Boost Your Tech Profile! Join Our DSA Courses for Advanced Algorithmic Mastery. Enroll Now to Stand Out in the Coding Landscape!

Conclusion

Let’s conclude our article by seeing the most important points that we have discussed in the whole article.

• When parsing mathematical expressions, three types of notations are commonly used : Infix Notation, Prefix Notation, and Postfix Notation.
• In Infix Notation, the operator is written in between the operands like (3+7), $(1*(2+3))$.
• In Prefix Notation, the operator should be present as a prefix or before the operands like $+37$, $*1(+23)$.
• In Postfix Notation, the operator should be present as a suffix, postfix, or after the operands like $37+$, $(23+)1*$.
• The modern Stack-organized computers are better suited for postfix and prefix notations than normally used infix notations due to their difficulty in parsing.