Problem Statement
We are provided with a sorted array of size n and we need to rearrange the array alternately. By rearrange array alternately, we should rearrange the array so that the first greatest element will come at the first position, and the first smallest element comes at the second position. Similarly, the second greatest element comes at the third position, the second minimum value comes at the fourth position, and so on.
Refer to the Example and Example Explanation sections for more details and the Approach section to understand how to rearrange array alternately.
Example
Example 1: The given sorted input array is:
[ 1, 2, 3, 4, 5, 6, 7 ]
After rearranging the array alternatively, the output comes out to be: [ 7, 1, 6, 2, 5, 3, 4 ]
Example 2: The given sorted input array is:
[ 1, 2, 3, 4, 5, 6 ]
After rearranging the array alternatively, the output comes out to be: [ 6, 1, 5, 2, 4, 3 ]
Refer to the next section for explanation of how to rearrange array alternately.
Example Explanation
Before getting into the explanation of the example of how to rearrange array alternately, we should briefly discuss arrays.
An array is a linear collection of values stored at contiguous memory locations. Array stores homogeneous values(similar data type values).
Let us take the first example provided above, the given sorted input array is: [ 1, 2, 3, 4, 5, 6, 7 ]
Now, we can see that the greatest element comes at last and the second greatest element comes just before that, and so on. Similarly, the smallest element comes at the first position, the second smallest element comes just after the greatest element, and so on.
So, in the output array, we will first insert the last element of the input array (which denotes the largest element of the input array). Then we will insert the first element of the input array (which denotes the smallest element of the input array).
Similarly, we will insert the second greatest element at the third position (in the output array), the second smallest element at the fourth position (in the output array), and so on. This process will continue until there is no element left to be inserted from the input array into the output array.
So, after rearranging the array alternatively, the output comes out to be: [ 7, 1, 6, 2, 5, 3, 4 ]
Refer to the Approach section, for more clarity and to understand the other approaches to rearrange array alternately.
Input/Output
- The first input is the number of elements present in the sorted array i.e. n.
- The second input is the sequential set of elements of the array.
Example: The given input array is: [ 1, 2, 3, 4, 5, 6, 7 ]
The output is:
Array formed after alternative rearrangement is:
7 1 6 2 5 3 4
Constraints
- 11 <= n <= 106106
- 11 <= array[i] <= 107107
In some problems, you may find the number of test cases represented by t. So, we only need to call the rearrangeArrayAlternatively() function t-times.
Note: The expected time and space complexity to solve the problem – rearrange array alternatively is:
- Expected Time Complexity: O(N).
- Expected Auxiliary Space: O(1).
Approach 1: Auxiliary Space Approach
The most basic approach to the problem – rearrange array alternately, can be using an extra output array of the same size as that of the input array (size = n) and then inserting the values from the input array into the output array alternatively.
The idea is quite simple, initialize an empty output array of size n (same as that of the input array). Then use two pointers namely i and j. The pointer i will be pointing at the index-0 which is the smallest element, and pointer j will be pointing at the last element i.e. index-n-1 which is the greatest element.
Now, we need another pointer let’s say k that will help traverse the output array. So, we will insert the largest element of the input array i.e. index j as the first element of the input array (pointing by index k). We will increment the index k of the input array and decrement the index j of the input array.
After that, we will insert the smallest element of the input array i.e. at index i as the second element of the input array (pointing by index k). We will increment the index k of the input array and increment the index i of the input array.
We will continue the above-stated process until we have traversed the entire input array (i.e. until i < j).
Algorithm
The pseudo-code for the above-discussed algorithm can be:
- Initialize two pointer i = 0 and j = n-1. So, pointer i will be pointing at the index-0 which is the smallest element, and pointer j will be pointing at the greatest element.
- Create an empty output[] array that will store the resultant rearranged array.
- Initialize the third pointer k = 0 which will be pointing at the index-0 of the output array.
- Start traversing the input array and copy the last element pointed by j at the index k of the output array.
- Increment the pointer k of the output array and decrement the pointer j of the input array.
- Similarly, copy the element pointed by i at the index k of the output array and increment the pointer k of the output array and increment the pointer i of the input array.
- Copy the steps (4 to 6) until the value of j is greater than the value of i.
Code Implementation
Let us code the above-discussed algorithm for better understanding.
C++
#include <bits/stdc++.h>
using namespace std;
void rearrangeArrayAlternatively(int a[], int n) {
// initializing output array of size-n
int output[n];
// initializing the pointers
int i = 0, j = n - 1, k = 0;
// inserting element from input array until i<= j
while (i <= j) {
// inserting the current greatest element and moving pointers of input and output array.
output[k++] = a[j--];
// inserting the current smallest element and moving pointers of input and output array
output[k++] = a[i++];
}
for (int i = 0; i < n; i++)
cout << output[i] << " ";
}
int main() {
int a[] = {1, 2, 3, 4, 5, 6};
int n = sizeof(a) / sizeof(a[0]);
cout << "Array formed after alternative rearrangement is: " << endl;
rearrangeArrayAlternatively(a, n);
return 0;
}
Java
public class Test {
static void rearrangeArrayAlternatively(int a[], int n) {
// initializing output array of size-n
int output[] = new int[n];
// initializing the pointers
int i = 0, j = n - 1, k = 0;
// inserting element from input array until i<= j
while (i <= j) {
// inserting the current greatest element and moving pointers of input and output array.
output[k++] = a[j--];
// inserting the current smallest element and moving pointers of input and output array
output[k++] = a[i++];
}
for (i = 0; i < n; i++)
System.out.print(output[i] + " ");
}
public static void main(String args[]) {
int a[] = {1, 2, 3, 4, 5, 6};
int n = a.length;
System.out.println("Array formed after alternative rearrangement is: ");
rearrangeArrayAlternatively(a, n);
}
}
Python
from black import out
def rearrangeArrayAlternatively(a, n):
# initializing output array of size-n
output = []
# initializing the pointers
i = 0
j = n - 1
# appending the data into the output list or array until i<= j
while i < j:
# inserting the current greatest element and the current smallest element
output.append(a[j])
output.append(a[i])
# moving pointers of the input array.
j = j - 1
i = i + 1
for i in range(len(output)):
print(output[i], end=" ")
if __name__ == "__main__":
a = [1, 2, 3, 4, 5, 6]
print("Array formed after alternative rearrangement is: ")
rearrangeArrayAlternatively(a, len(a))
Output
Array formed after alternative rearrangement is:
6 1 5 2 4 3
In the brute force or basic approach to the problem – rearrange array alternately, we are traversing the input array only once using two pointers. We are using an extra array to store the result.
Time Complexity
Since we are traversing the input array only once, the time complexity of the brute force approach to the problem – rearrange array alternately comes out to be O(n), where n is the size of the input array.
Space Complexity
Since we are using an extra array to store the result, the space complexity of the brute force approach to the problem – rearrange array alternately comes out to be O(n), where n is the size of the output/input array.
Approach 2: Efficient Approach – Constant Space Approach
An efficient algorithm for the problem – rearrange array alternately, can be using multiplication and modular tricks to store the elements (two elements) at the same index.
For example, let us suppose the current array scenario i.e. [ 5, 7, 10 ]. Here n1 = 5, n2 = 7, and z = 10. Now in this example, z can be any number greater than the maximum element. So, z is pointing to 10.
Suppose that we have stored both n1 and n2 at a single index then we can use the modular operator (%) and the division operator (/) to get them back to the original numbers.
Let us see how.
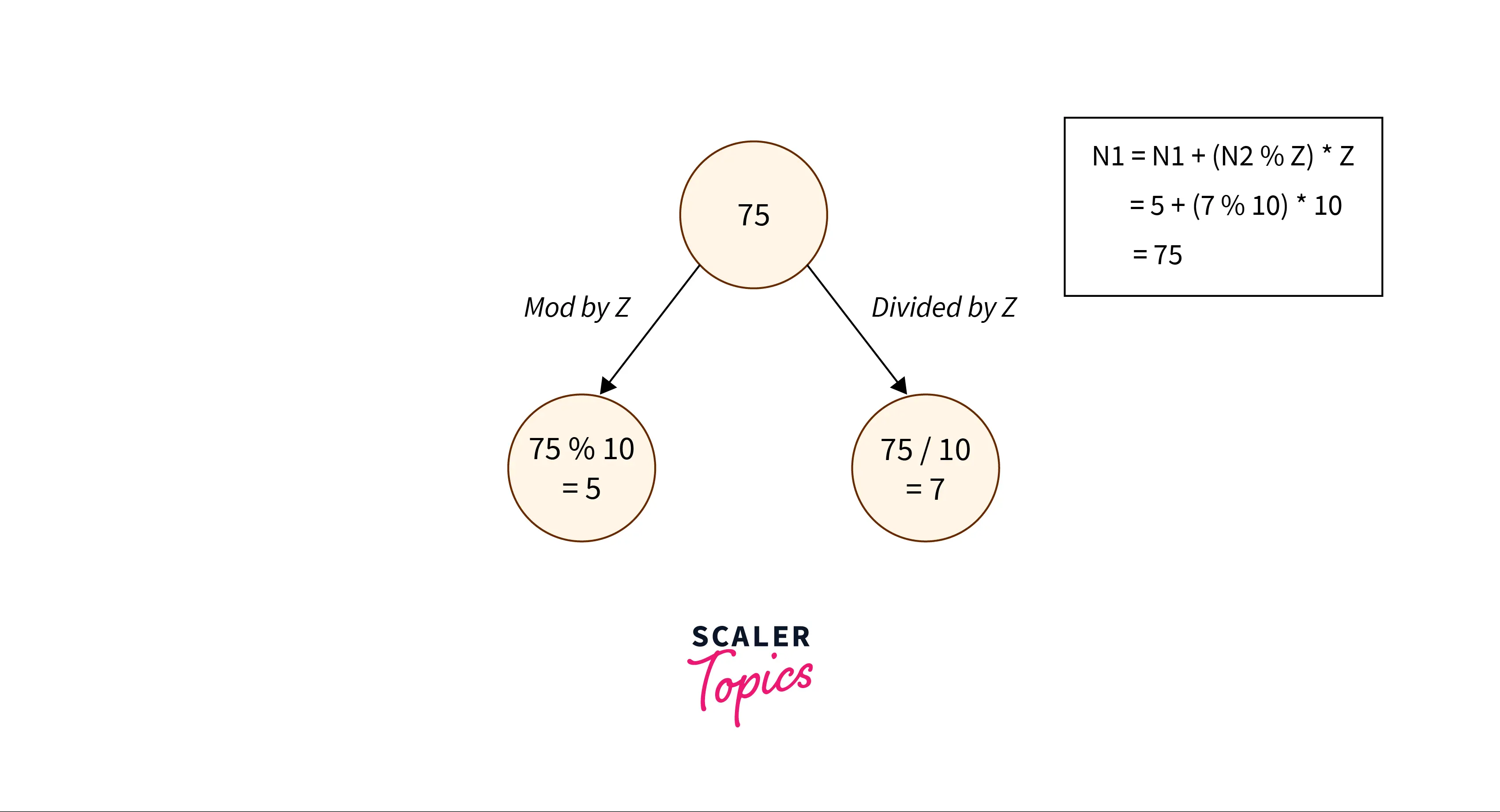
Refer to the pseudo code (shown below) for the steps.
Algorithm
The pseudo-code for the above-discussed algorithm can be:
- Initialize two pointers i and j, i will be pointing at the minimum index, and j will be pointing at the maximum index (i.e. n-1).
- Initialize another variable called greaterMax that will be equal to the 1 + maximum element i.e. 1 + a[j].
- Traverse the entire input array by performing the following operations:
- check if the current index is even (divisible by 2), then:
- update a[currentIndex] = a[currentIndex] + (A[j] % greaterMax) * greaterMax
- decrement j by 1 i.e. j–
- if the current index is odd (not divisible by 2), then:
- update a[currentIndex] = a[currentIndex] + (A[i] % greaterMax) * greaterMax
- increment i by 1 i.e. i++
- check if the current index is even (divisible by 2), then:
Code Implementation
Let us code the above-discussed algorithm for better understanding.
C++
#include <bits/stdc++.h>
using namespace std;
void rearrangeArrayAlternatively(int a[], int n) {
// initializing the pointers
int j = n - 1, i = 0;
// storing the maximum element of the array
int greaterMax = a[n - 1] + 1;
// traversing array elements
for (int index = 0; index < n; index++) {
// check if the current index is even
if (index % 2 == 0) {
// update the a[index] element
a[index] += (a[j] % greaterMax) * greaterMax;
// decrement j by 1
j--;
}
// if the current index is odd
else {
// update the a[index] element
a[index] += (a[i] % greaterMax) * greaterMax;
// increment i by 1
i++;
}
}
// To update the array element back to its original form, divide a[i] by greaterMax
for (i = 0; i < n; i++)
cout << a[i] / greaterMax << " ";
}
int main() {
int a[] = {1, 2, 3, 4, 5, 6};
int n = sizeof(a) / sizeof(a[0]);
cout << "Array formed after alternative rearrangement is: " << endl;
rearrangeArrayAlternatively(a, n);
return 0;
}
Java
public class Test {
static void rearrangeArrayAlternatively(int a[], int n) {
// initializing the pointers
int j = n - 1, i = 0;
// storing the maximum element of the array
int greaterMax = a[n - 1] + 1;
// traversing array elements
for (int index = 0; index < n; index++) {
// check if the current index is even
if (index % 2 == 0) {
// update the a[index] element
a[index] += (a[j] % greaterMax) * greaterMax;
// decrement j by 1
j--;
}
// if the current index is odd
else {
// update the a[index] element
a[index] += (a[i] % greaterMax) * greaterMax;
// increment i by 1
i++;
}
}
// To update the array element back to its original form, divide a[i] by greaterMax
for (i = 0; i < n; i++)
System.out.print(a[i]/greaterMax + " ");
}
public static void main(String args[]) {
int a[] = {1, 2, 3, 4, 5, 6};
int n = a.length;
System.out.println("Array formed after alternative rearrangement is: ");
rearrangeArrayAlternatively(a, n);
}
}
Python
def rearrangeArrayAlternatively(a, n):
# initializing the pointers
i = 0
j = n - 1
# storing the maximum element of the array
greaterMax = a[n - 1] + 1
for index in range(len(a)):
# check if the current index is even
if (index % 2 == 0):
# update the a[index] element
a[index] += (a[j] % greaterMax) * greaterMax
# decrement j by 1
j = j - 1
else:
# if the current index is odd
# update the a[index] element
a[index] += (a[i] % greaterMax) * greaterMax
# increment i by 1
i = i + 1
for i in range(len(a)):
print(a[i]//greaterMax, end=" ")
if __name__ == "__main__":
a = [1, 2, 3, 4, 5, 6]
print("Array formed after alternative rearrangement is: ")
rearrangeArrayAlternatively(a, len(a))
Output
Array formed after alternative rearrangement is:
6 1 5 2 4 3
In the constant space approach to the problem – rearrange array alternately, we are traversing the input array only once using two pointers. We are not using any extra space to store the result.
Time Complexity
Since we are traversing the input array only once, the time complexity of the constant space approach to the problem – rearrange array alternately comes out to be O(n), where n is the size of the input array.
Space Complexity
Since we are not using any extra array to store the result, the space complexity of the constant space approach to the problem – rearrange array alternatelyy comes out to be O(1).
Approach 3: Simpler approach – Observing indexing positioning of maximum elements and minimum elements
Another efficient yet simple algorithm to the problem -rearrange array alternately can be focusing on the maximum element’s index and minimum element’s index. The maximum elements will be stored at the even indices of the array while the minimum elements will be stored at the odd indices of the array. So, we will traverse the array only once and store the array elements at specific positions.
Note: We should keep in mind that the above approach only works when the provided sorted input array is consecutive. i.e. the elements of the array vary by 1 only.
Code Implementation
Let us code the above-discussed algorithm for better understanding.
C++
#include <bits/stdc++.h>
using namespace std;
void rearrangeArrayAlternatively(int a[], int n) {
// initializing the pointers
int j = a[n - 1];
int i = a[0];
// traversing the input array
for (int index = 0; index < n; index++) {
// putting the maximum element at the even position
if (index % 2 == 0) {
a[index] = j;
j -= 1;
}
// putting the minimum element at the odd position
else {
a[index] = i;
i += 1;
}
}
// traversing the array and printing it
for (int i = 0; i < n; i++)
cout << a[i] << " ";
}
int main() {
int a[] = {1, 2, 3, 4, 5, 6};
int n = sizeof(a) / sizeof(a[0]);
cout << "Array formed after alternative rearrangement is: " << endl;
rearrangeArrayAlternatively(a, n);
return 0;
}
Java
public class Test {
static void rearrangeArrayAlternatively(int a[], int n) {
// initializing the pointers
int j = a[n - 1];
int i = a[0];
// traversing the input array
for (int index = 0; index < n; index++) {
// putting the maximum element at the even position
if (index % 2 == 0) {
a[index] = j;
j -= 1;
}
// putting the minimum element at the odd position
else {
a[index] = i;
i += 1;
}
}
// traversing the array and printing it
for (i = 0; i < n; i++)
System.out.print(a[i] + " ");
}
public static void main(String args[]) {
int a[] = { 1, 2, 3, 4, 5, 6 };
int n = a.length;
System.out.println("Array formed after alternative rearrangement is: ");
rearrangeArrayAlternatively(a, n);
}
}
Python
def rearrangeArrayAlternatively(a, n):
# initializing the pointers
i = a[0]
j = a[n - 1]
# traversing the input array
for index in range(n):
# putting the maximum element at the even position
if (index % 2 == 0):
a[index] = j
j = j - 1
else:
# putting the minimum element at the odd position
a[index] = i
i = i + 1
# traversing the array and printing it
for i in range(n):
print(a[i], end=" ")
if __name__ == "__main__":
a = [1, 2, 3, 4, 5, 6]
print("Array formed after alternative rearrangement is: ")
rearrangeArrayAlternatively(a, len(a))
Output
Array formed after alternative rearrangement is:
6 1 5 2 4 3
In the indexing positioning of maximum elements and minimum elements approach to the problem – rearrange array alternately, we are traversing the input array only once using two pointers. We are not using any extra space to store the result.
Time Complexity
Since we are traversing the input array only once, the time complexity of the indexing positioning of maximum elements and minimum elements approach to the problem – rearrange array alternately comes out to be O(n), where n is the size of the input array.
Space Complexity
Since we are not using any extra array to store the result, the space complexity of the indexing positioning of maximum elements and minimum elements approach to the problem – rearrange array alternately comes out to be O(1).
Conclusion
- The most basic approach to the problem – rearrange array alternately can be using an extra output array of size = n and then inserting the values from the input array to the output array alternatively.
- In the brute force approach to the problem – rearrange array alternately, the time complexity comes out to be O(n), where n is the number of elements present in the array. The space complexity is O(n) as we are using an extra array.
- An efficient algorithm for the problem – rearrange array alternately can be using multiplication and modular tricks to store the elements (two elements) at the same index.
- In the constant space approach to the problem – rearrange array alternately, the time complexity comes out to be O(n), where n is the number of elements present in the array. The space complexity is O(1) as we are not using any extra space.
- Another efficient algorithm for the problem – rearrange array alternately can be storing the maximum elements at the even indices of the array while the minimum elements will be stored at the odd indices of the array.
- In the indexing positioning of maximum elements and minimum elements approach to the problem – rearrange array alternately, the time complexity comes out to be O(n), where n is the number of elements present in the array. The space complexity is O(1) as we are not using any extra space.