Splay Tree in data structures is a type of binary search tree that uses a splaying operation on the tree so the most frequently used elements can come closer to the root. This increases the insertion, deletion, and search operations in the tree.
Scope of the Article
- This article defines a splay tree, its properties, operations on a splay tree, and the implementation of a splay tree in C/C++/Java/Python.
- You will see different types of rotations performed on the splay tree.
- You will also see the advantages and disadvantages of the splay tree.
Introduction to Splay Tree
As we know, the worst-case time complexity of operations like search, delete, and insert on a binary search tree is O(n), while the average time complexity is O(logn). The value of the left subtree in a binary search tree is smaller than the value of the root node, and the value of the right subtree is greater than the value of the root node. The time complexity, in this case, would be O(logn), and if we tried to skew left or right, the time complexity would be O(logn). We can reduce skewness by using AVL and Red-Black trees and can reduce complexity to O(logn).
But, can we do better than this?
The answer is YES. But how?
Here comes the concept of “Splay Tree”.
Note: If you are reading this article, then I will suggest that you should know about binary search trees. At least you know the basics of binary search trees, like how to search, delete, and insert operations are performed.
What is Splay Tree?
Have you ever thought that AVL and Red-Black trees are also self-adjusted trees? Then, what makes the Splay Tree different from the AVL and Red-Black trees? Yes, there is one operation called splaying, which makes it different from both AVL and the Red-Black Tree.
A splay tree contains all the operations of a binary search tree, like insertion, deletion, and searching. But it also contains one more operation, which is called splaying. In a splay tree, every operation is performed at the root of the tree. All operations in the splay tree involve one common operation called splaying.
You may have questioned what splaying is and why it differentiates splay trees from AVL and Red-Black trees. So, let me tell you about splaying. Splaying is the process of bringing an element to the root by performing suitable rotations.
By splaying elements in the tree, we can bring more frequently used elements closer to the root of the tree so that any operations like insertion, searching, and deletion can be performed quickly. This means, that after applying the splaying operation, more frequently used elements come closer to the root.
Suppose we have been given a binary search tree with different nodes and we know that in the binary search tree, elements to the left are smaller and those to the right are greater than the root node.
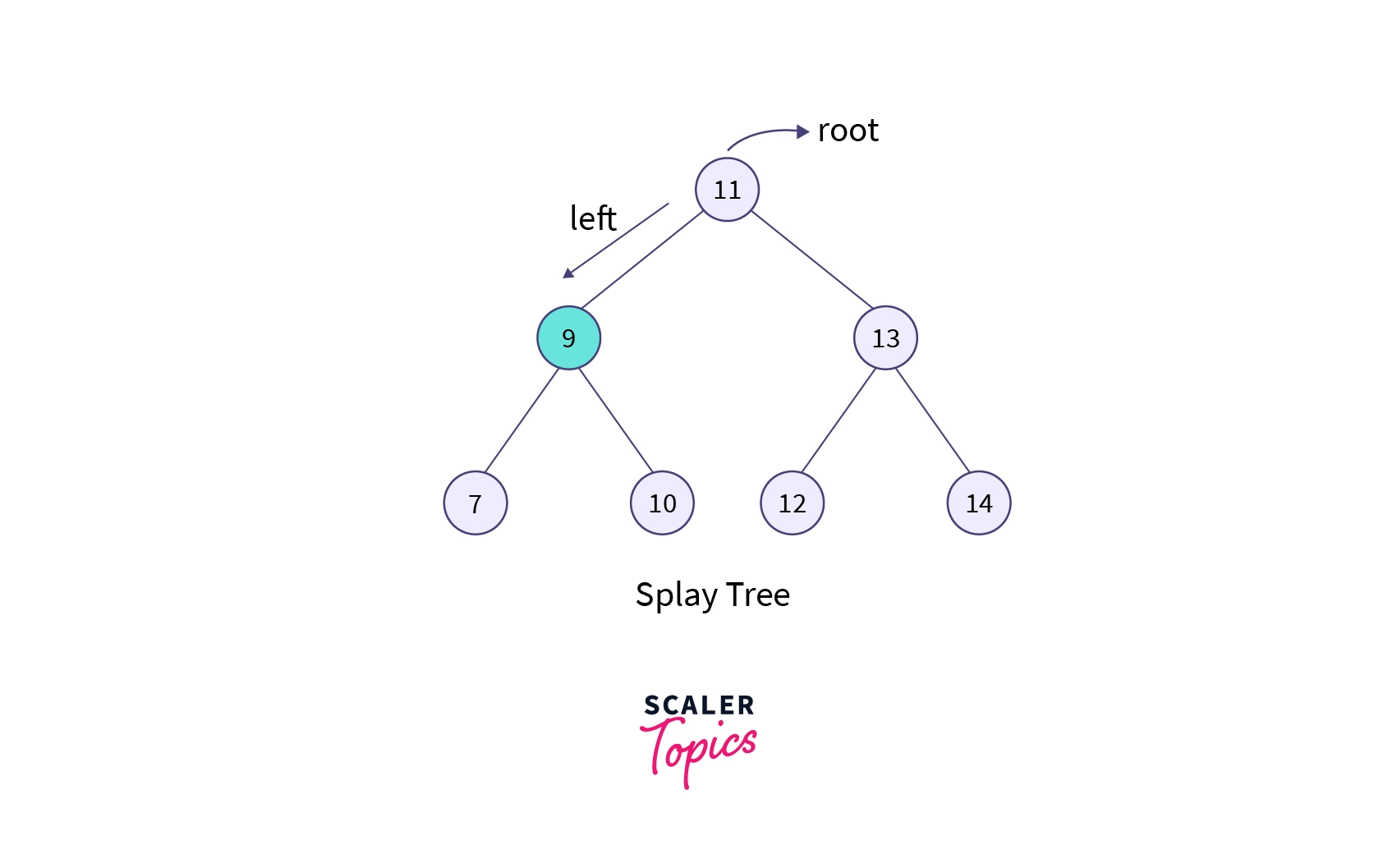
For searching, we will perform the binary search method. Let’s say we want to search for element 9. As 9 is less than 11, we will come to the left of the root node. After performing a search operation, we need to do one thing called splaying. This means, that after splaying, the element on which we are operating should come to the root. Elements would come to the root after performing some rearrangements of elements or rotations in the tree.
Rotations in Splay Tree
To rearrange the tree, we need to perform some rotations. The rotations given below are the rotations that we are going to perform in the splay tree.
- Zig rotation [Right Rotation]
- Zig zig [Two Right Rotations]
- Zag rotation [Left Rotation]
- Zag zag [Two Left Rotations]
- Zig zag [Zig followed by Zag]
- Zag zig [Zag followed by Zig]
Zig rotation:
This rotation is similar to the right rotation in the AVL tree. In zig rotation, every node moves one position to the right of its current position. We use Zig rotation when the item which is to be searched is either a root node or a left child of the root node.
Let’s take a scenario where the search item is the left child of the root node.
In the above example, we have to search for node 9 in the tree. To search for the given node in the binary search tree, we need to perform the following steps:
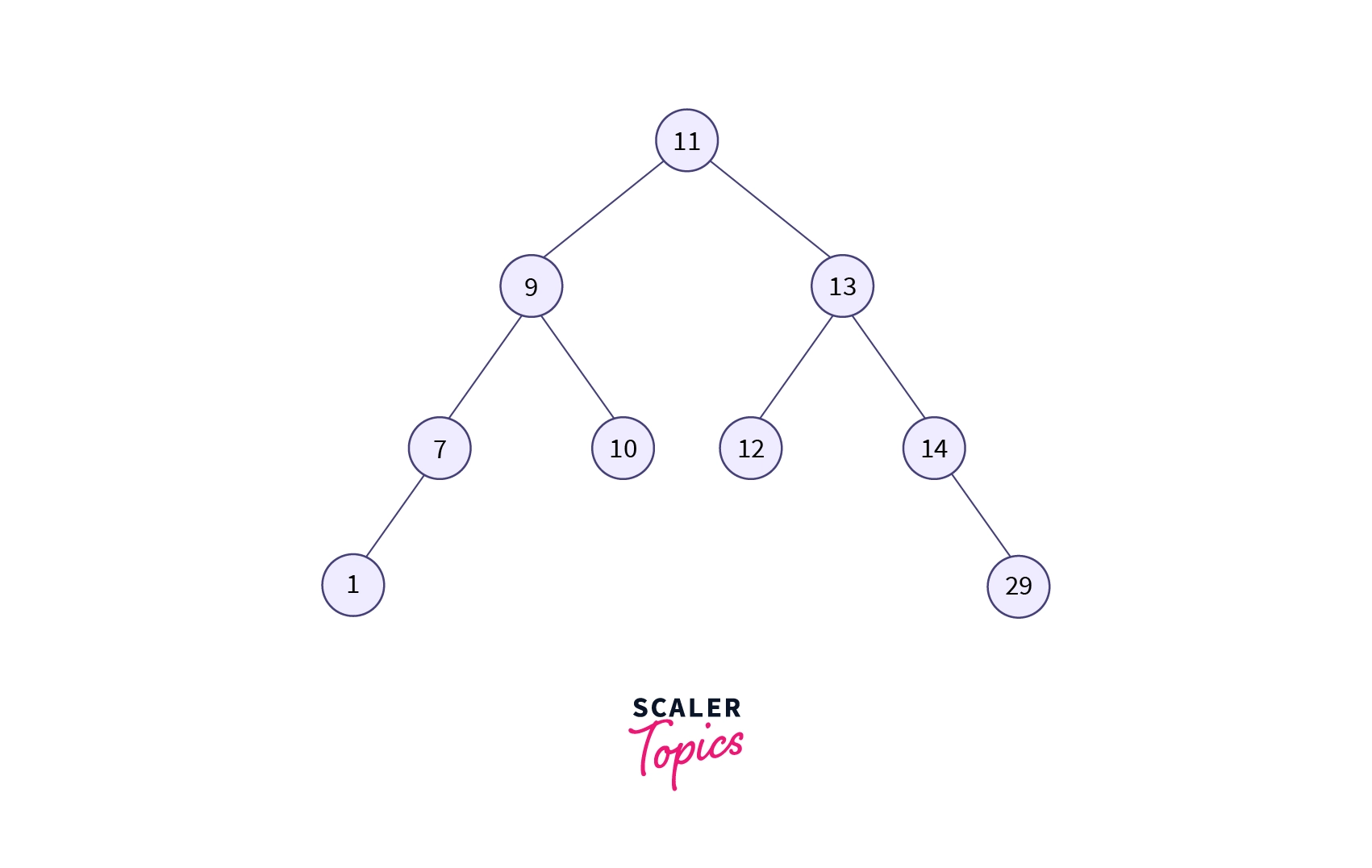
Step 1: First, we compare 9 with the root node. As 9 is less than 11, it is a left child of the root node.
Step 2: We have already seen above that once the element is found, we will perform splaying. Here the right rotation is performed so that 9 becomes the root node of the tree. Have a look at the diagram below.
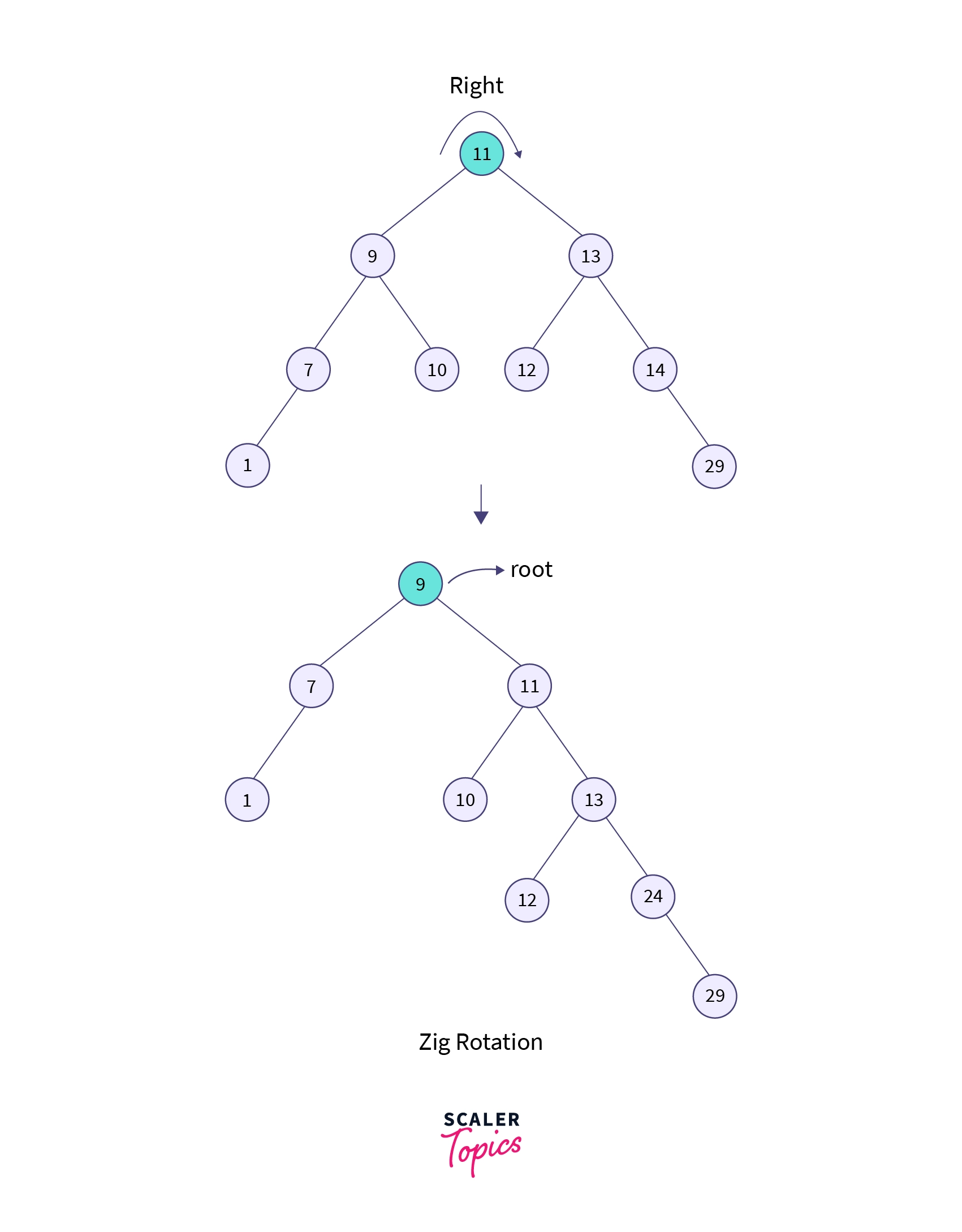
In the above diagram, we can see that node 9 has become the root node of the tree, this shows that the searching is completed.
Zig zig rotation:
It’s a kind of double zig rotation. Here we perform zig rotation two times. Every node moves two positions to the right of its current position. But why are we doing this?
We are doing this because sometimes situations arise where we need to search for the item that has both parent and grandparent. In such cases, we have to perform four rotations for splaying.
In the example given below, suppose we have to search for element 3.
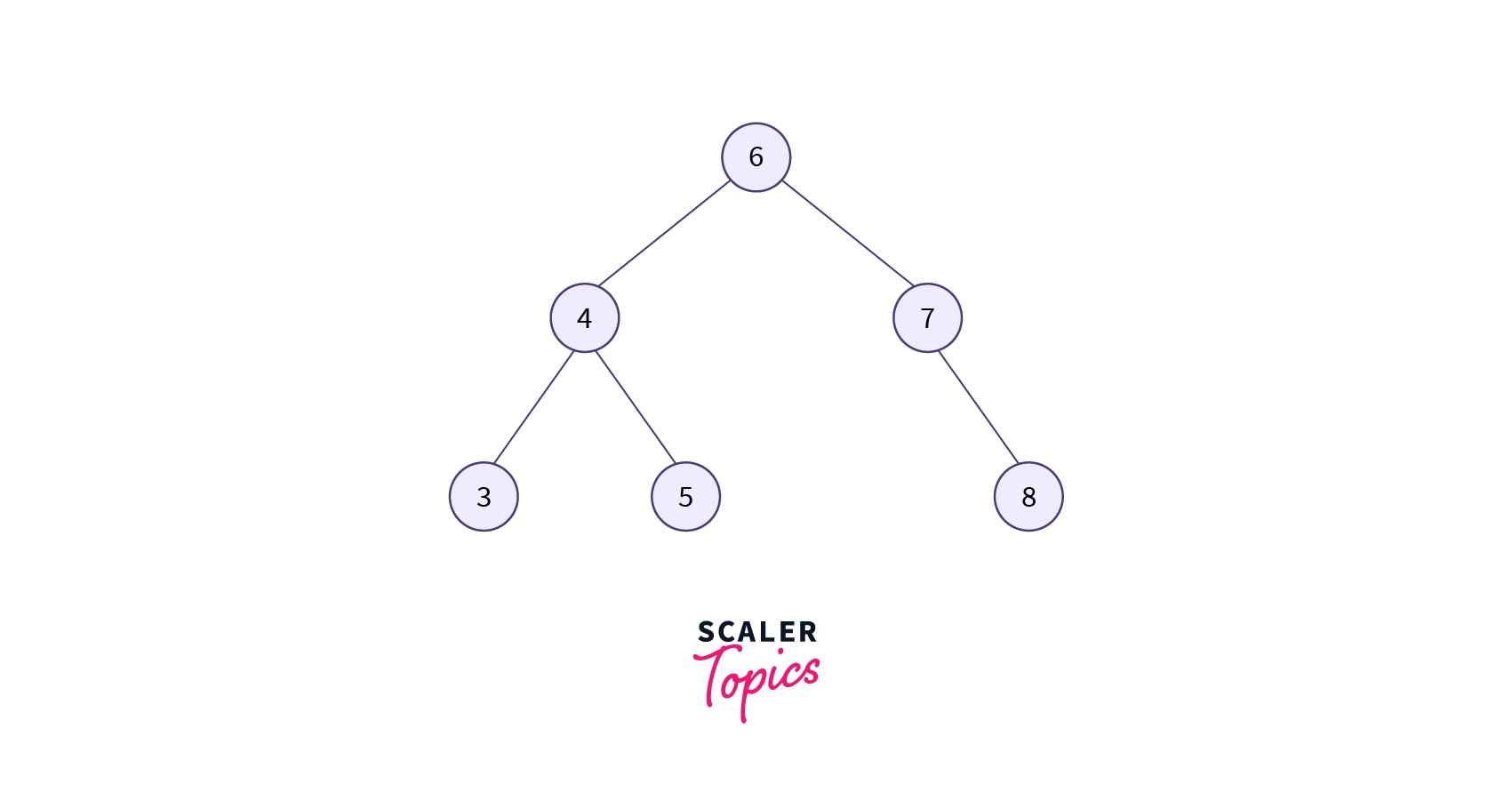
Step 1: First, we have to perform a search operation in the tree as we did previously, which means a BST operation. As 3 is less than 6 and 4, it will be at the left of node 4. So we can say that element 3 has a parent of 4 and a grandparent of 6.
Step 2: We have to perform splaying, which means we have to make node 3 the root node. So here we will perform two right rotations because the elements to be searched have both parent and grandparent.
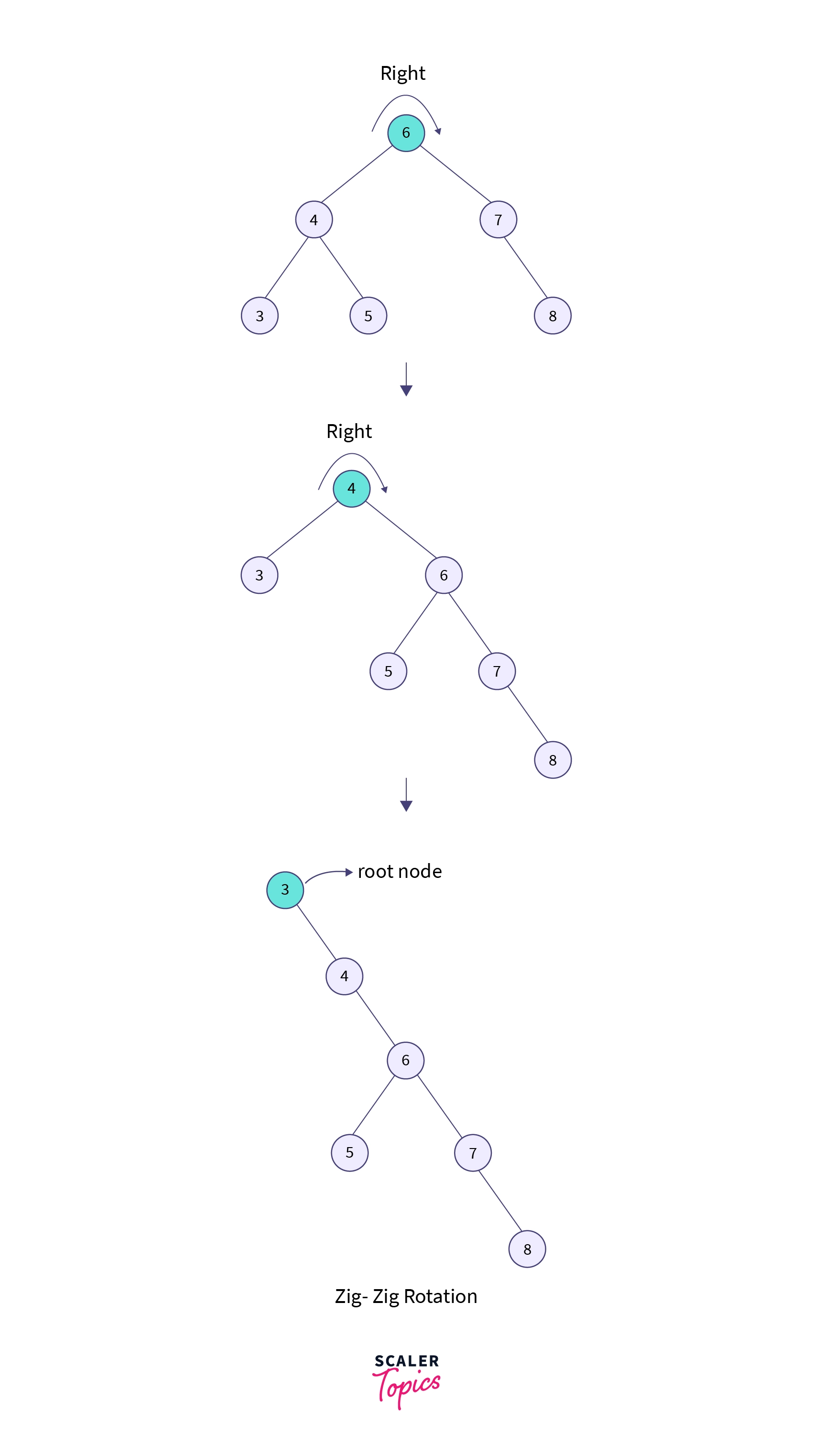
In the above diagram, we can see that node 3 has become the root node of the tree, this shows that the searching is completed.
Zag rotation:
This rotation is similar to the left rotation in the AVL tree. In zag rotation, every node moves one position to the left of its current position. We use Zag rotation when the item which is to be searched is either a root node or a right child of the root node.
Let’s see the case where the element to be searched for is present on the right of the root node of the tree. Now let’s say we have to search for 13, which is present on the right of the root node of the tree.
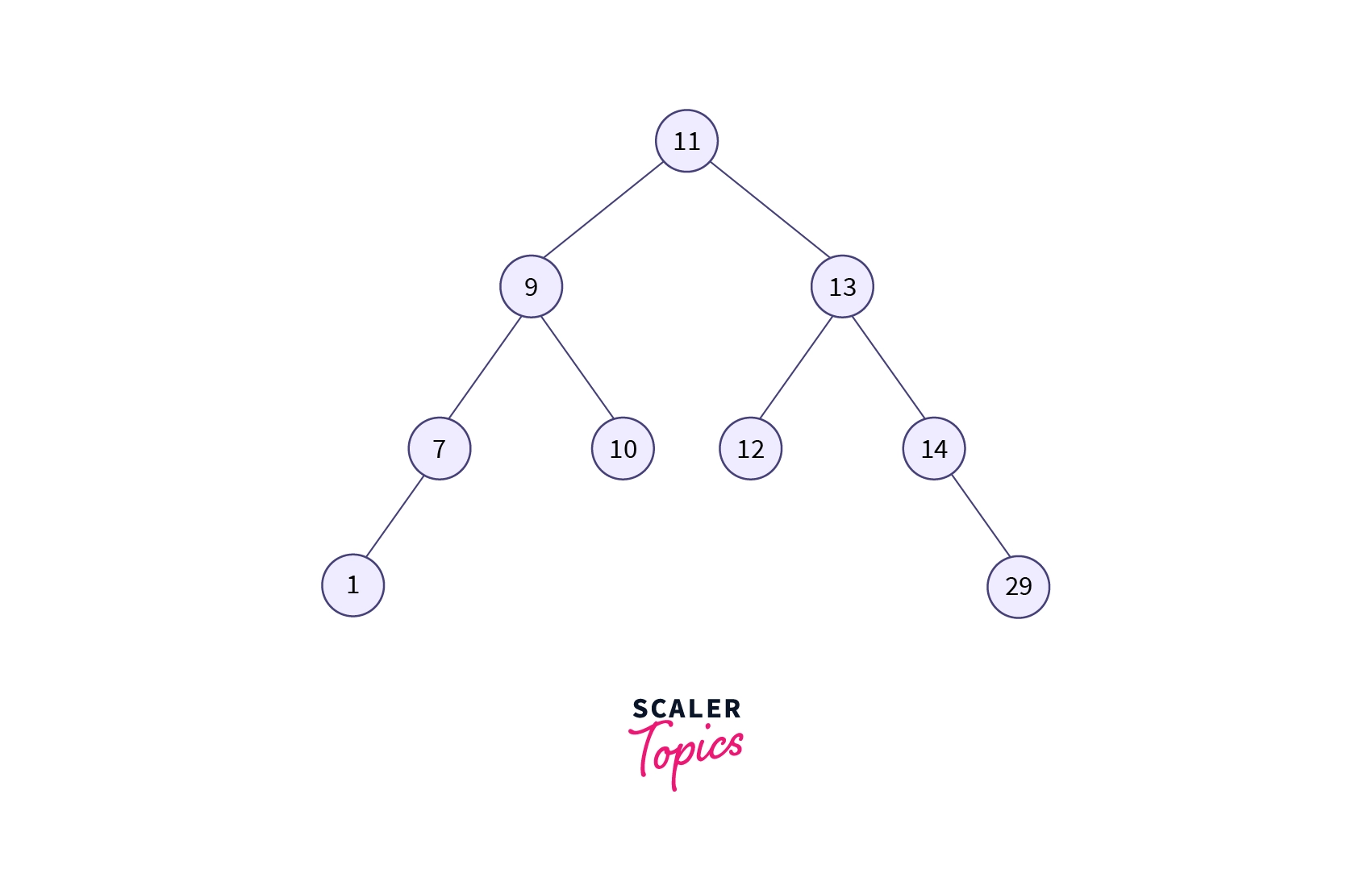
The steps involved in searching are given below:
Step 1: First, we compare 13 with the root node. As 13 is greater than the root node of the tree, it is the right child of the root node.
Step 2: Once the element is found, we will perform splaying as we did in the previous examples. Here we will perform a left rotation so that 13 becomes the root node of the tree.
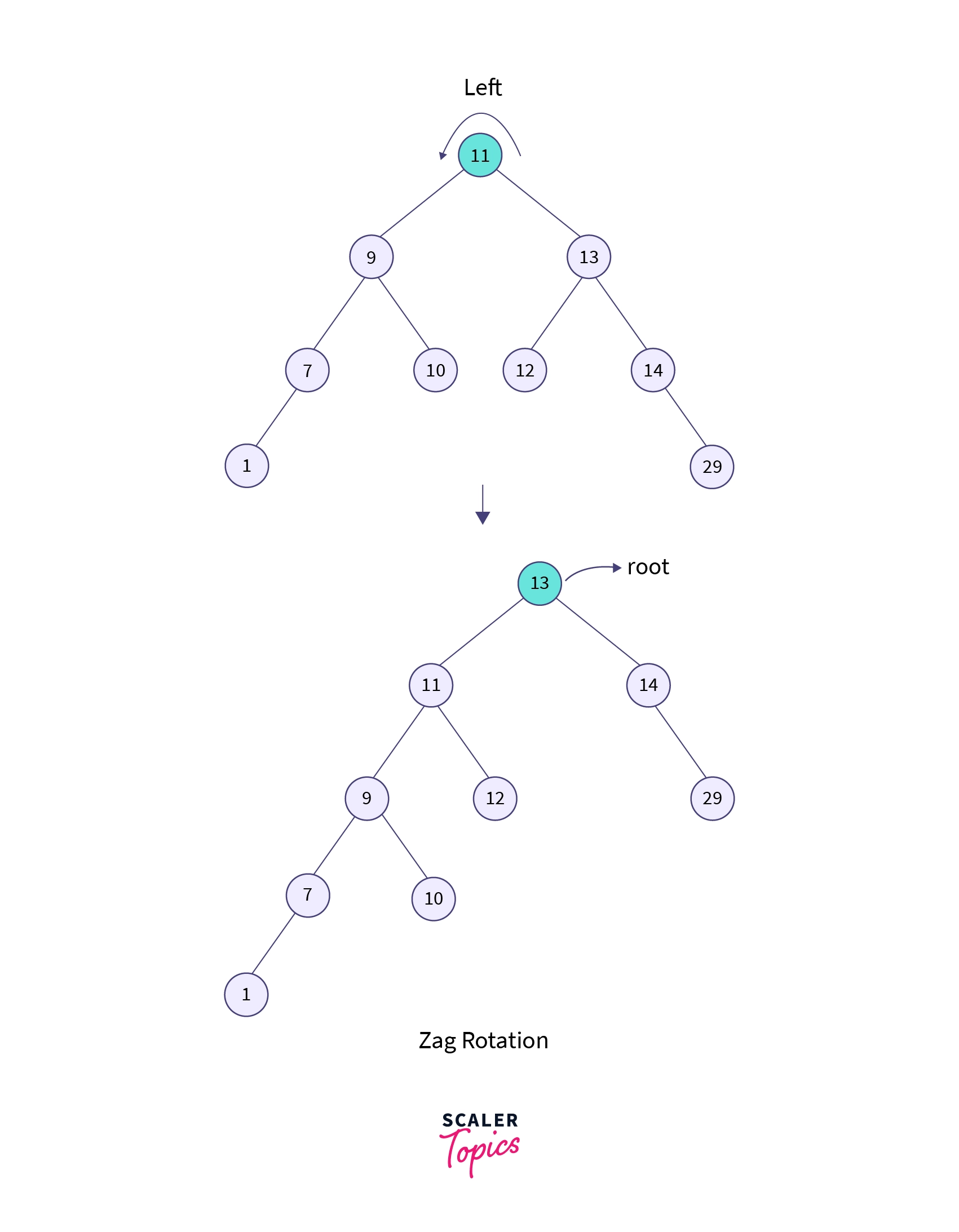
In the above diagram, we can see that node 13 has become the root node of the tree, this shows that the searching is completed.
Zag Zag Rotation:
It’s a kind of double zag rotation. Here we perform zag rotation two times. Every node moves two positions to the left of its current position. But why are we doing this?
We are doing this because sometimes situations arise where we need to search for the item that has both parent and grandparent. In such cases, we have to perform four rotations for splaying.
Now we will try to understand this case with some examples:
In the example given below, suppose we have to search for element 7.
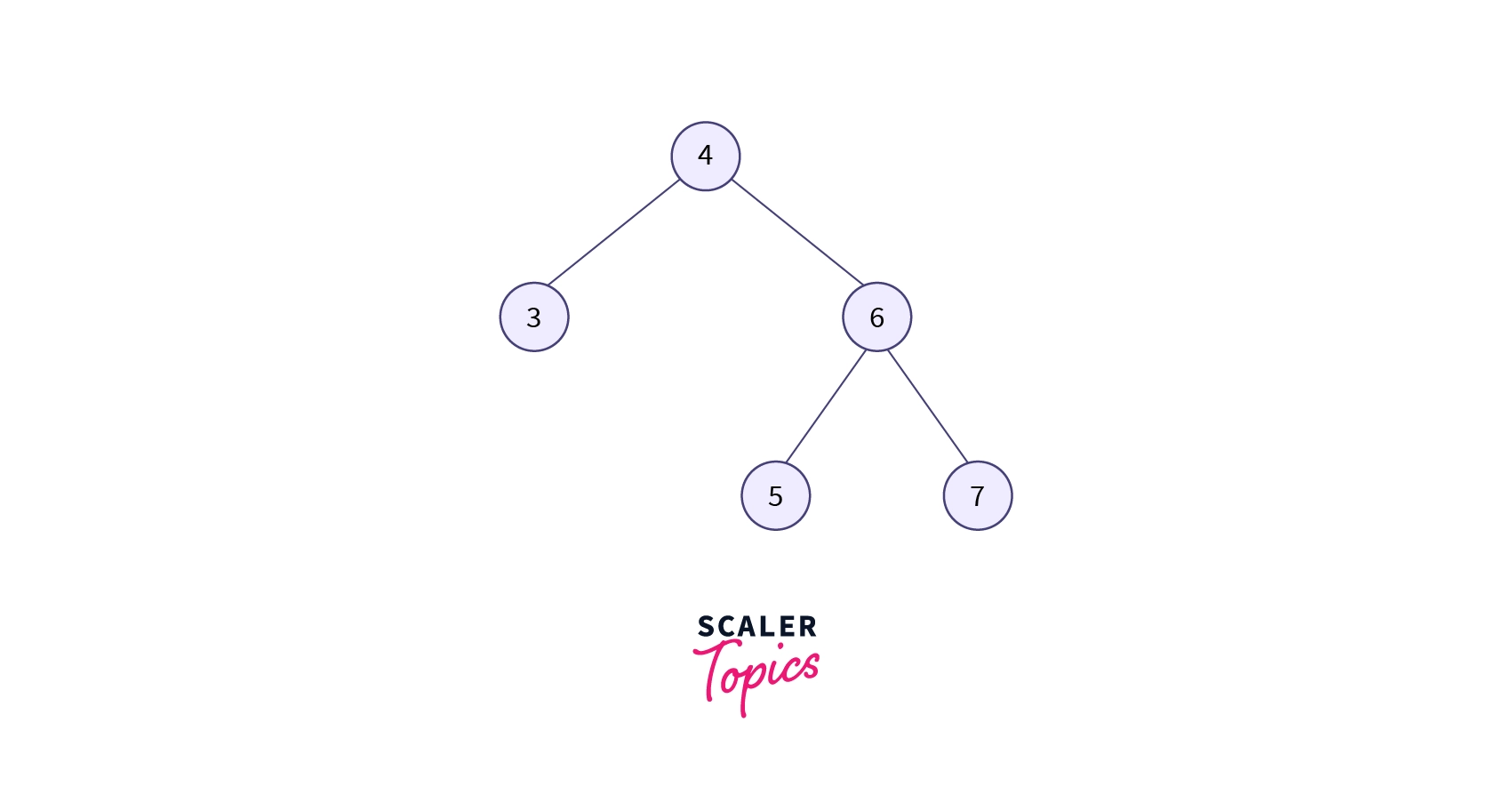
Step 1: First, we have to perform a search operation in the tree as we did previously, which means a BST operation. As 7 is greater than 4 and 6, it will be at the right of node 6. So we can say that element 7 has a parent of 6 and a grandparent of 4.
Step 2: We have to perform splaying, which means we have to make node 7 the root node. So here we will perform two left rotations because the elements to be searched have both parent and grandparent.
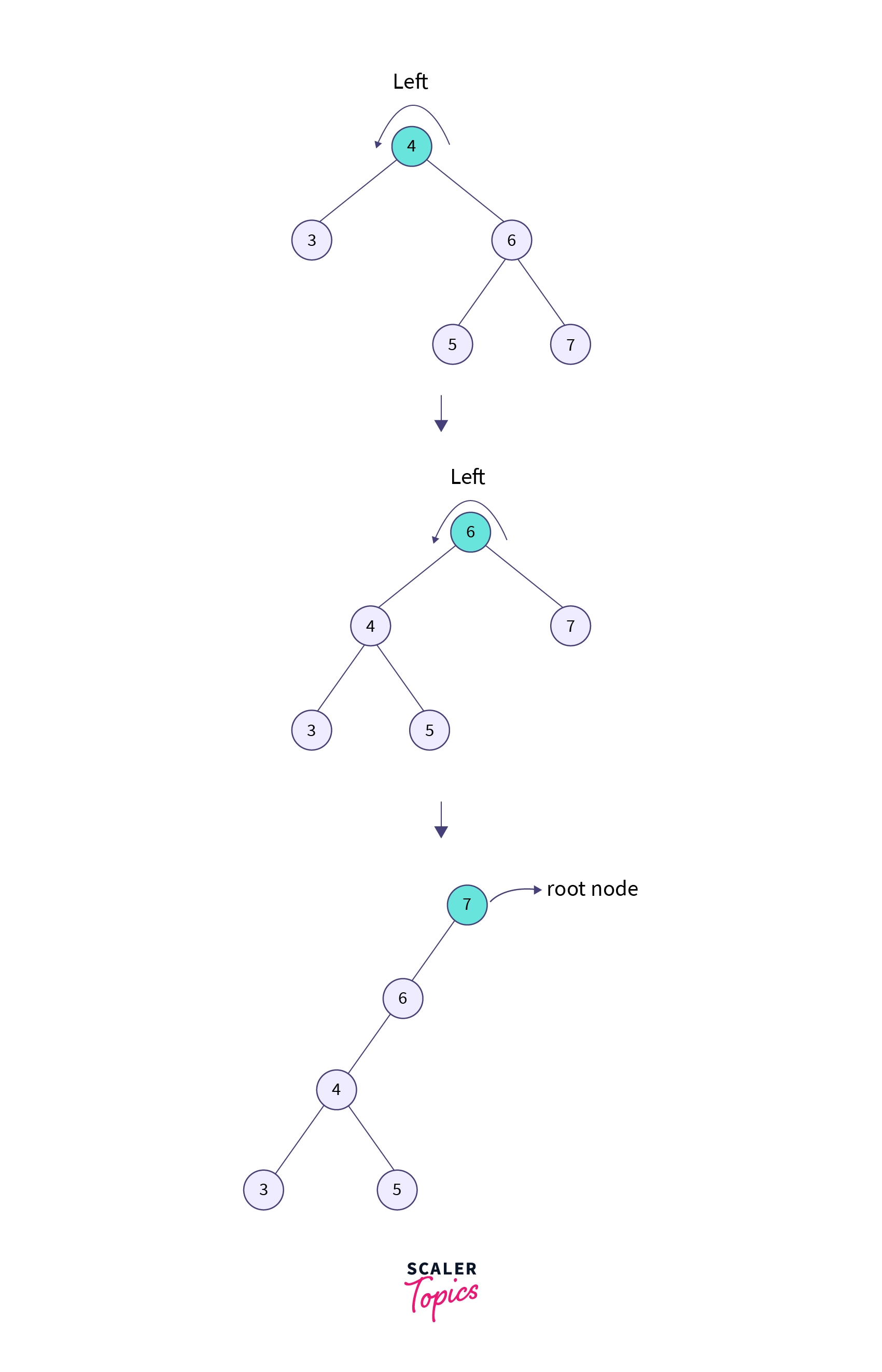
In the above diagram, we can see that node 7 has become the root node of the tree, this shows that the searching is completed.
Zig Zag rotation
This type of rotation is a sequence of zig rotations followed by zag rotations. So far, we’ve seen that both the parent and the grandparent are in a RR or LL relationship. Now, here we will see the RL and LR kinds of relationships between parent and grandparent. Every node moves one position to the right, followed by one position to the left of its current position.
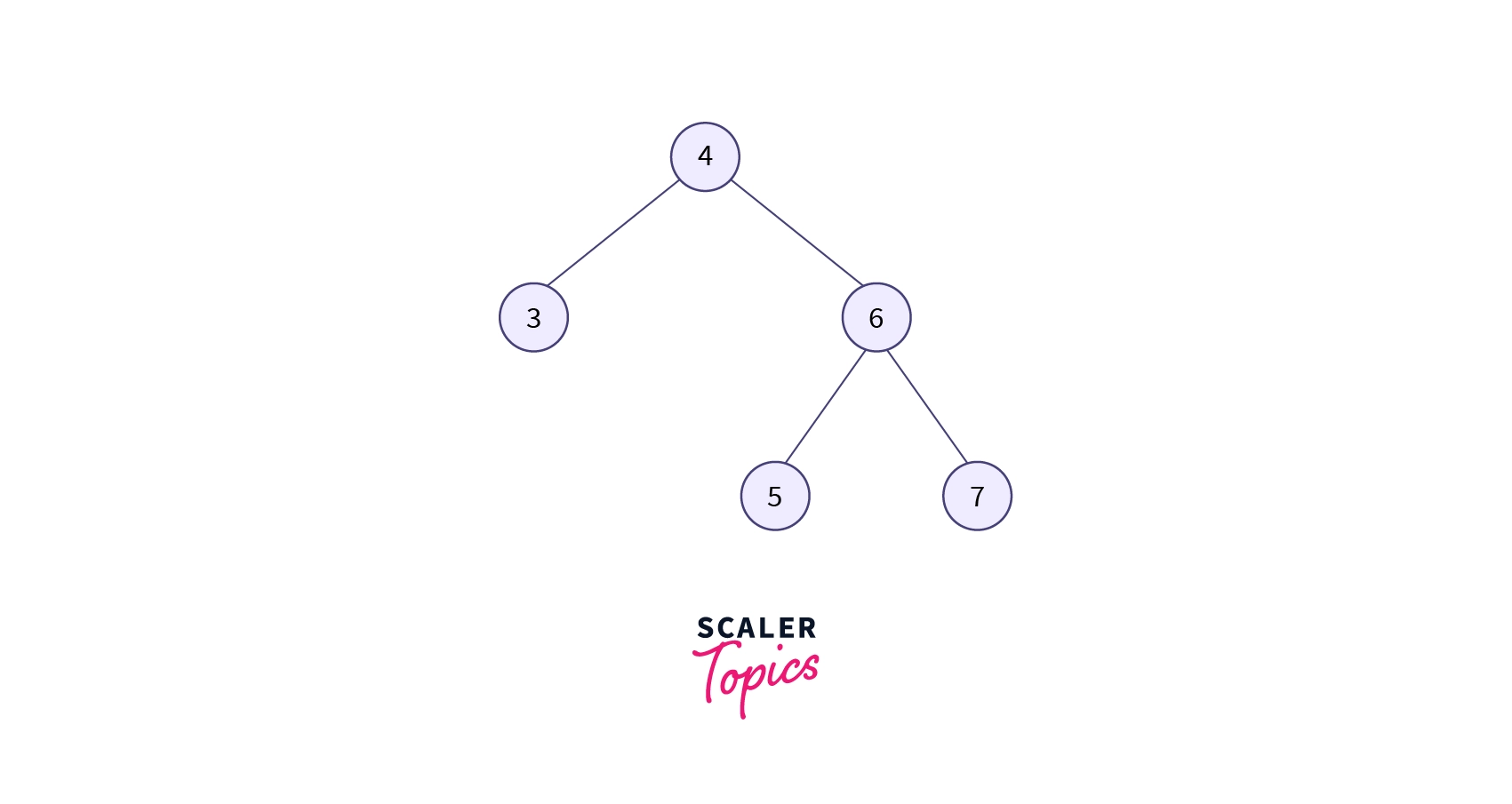
Suppose we want to search for element 5. Here first we perform a BST searching operation. Like 5, it is greater than the root node 4 and smaller than the node 6. So 5 would be the left child of node 6.
So an RL relationship exists since node 5 is to the left of node 6 and node 6 is to the right of node 4. So first we will perform the right rotation on node 6, and then node 6 will move downwards, and node 5 will come upwards, as you can see in the example given below. After that, we will perform zag rotation(left rotation) at 4, and we will see that 5 will become the root node of the tree.
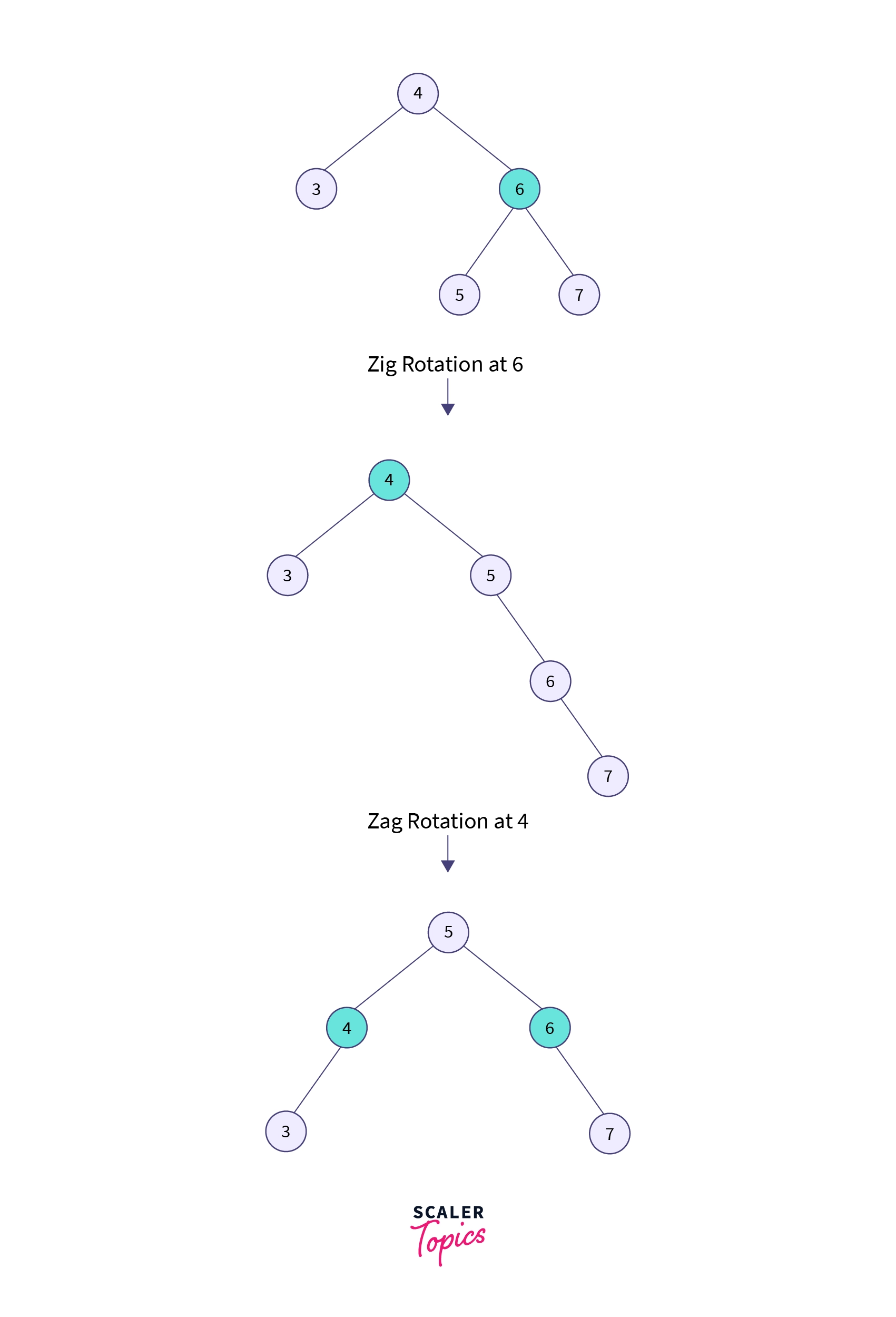
As we can observe in the above tree, node 5 has become the root node; therefore, the search is completed. In this case, first, we have performed the zig rotation and then the zag rotation. So it is known as zig-zag rotation.
Zag Zig Rotation
This rotation is similar to the Zig-zag rotation, the only difference is that here every node moves one position to the left, followed by one position to the right of its current position.
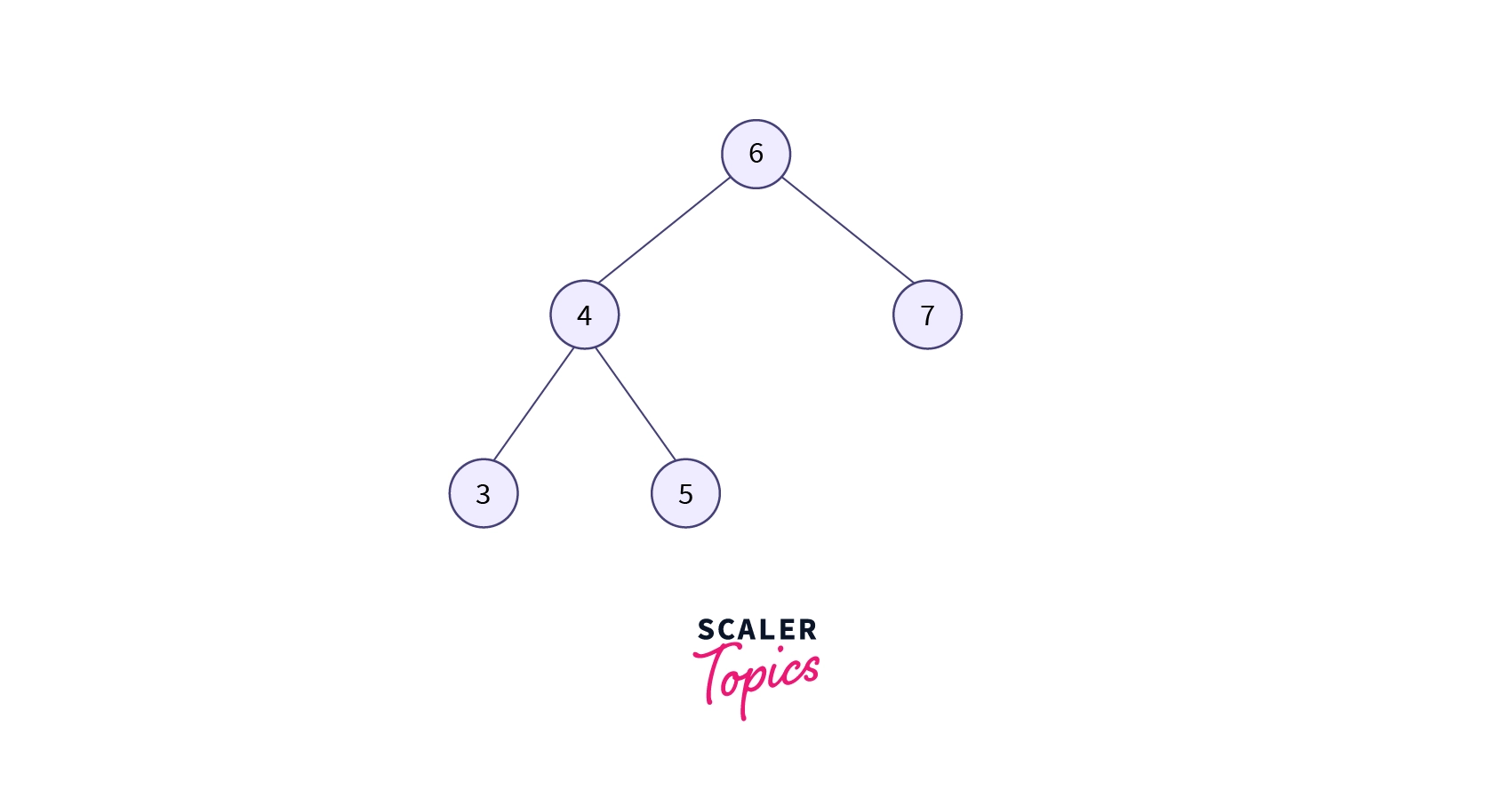
Suppose we want to search for element 5. Here first we perform a BST searching operation. Like 5, it is smaller than the root node 6 and greater than node 4. So 5 would be the right child of node 4, and 4 would be the left child of the root node 6.
So here $LR$ relationship exists since node 5 is to the right of node 4 and node 4 is to the left of node 6. So first we will perform the left rotation on node 4, and then node 4 will move downwards, and node 5 will come upwards, as you can see in the example given below. And after that, we will perform one zig rotation (right rotation) at 6, so finally, we will get 5 as the root node of the tree.
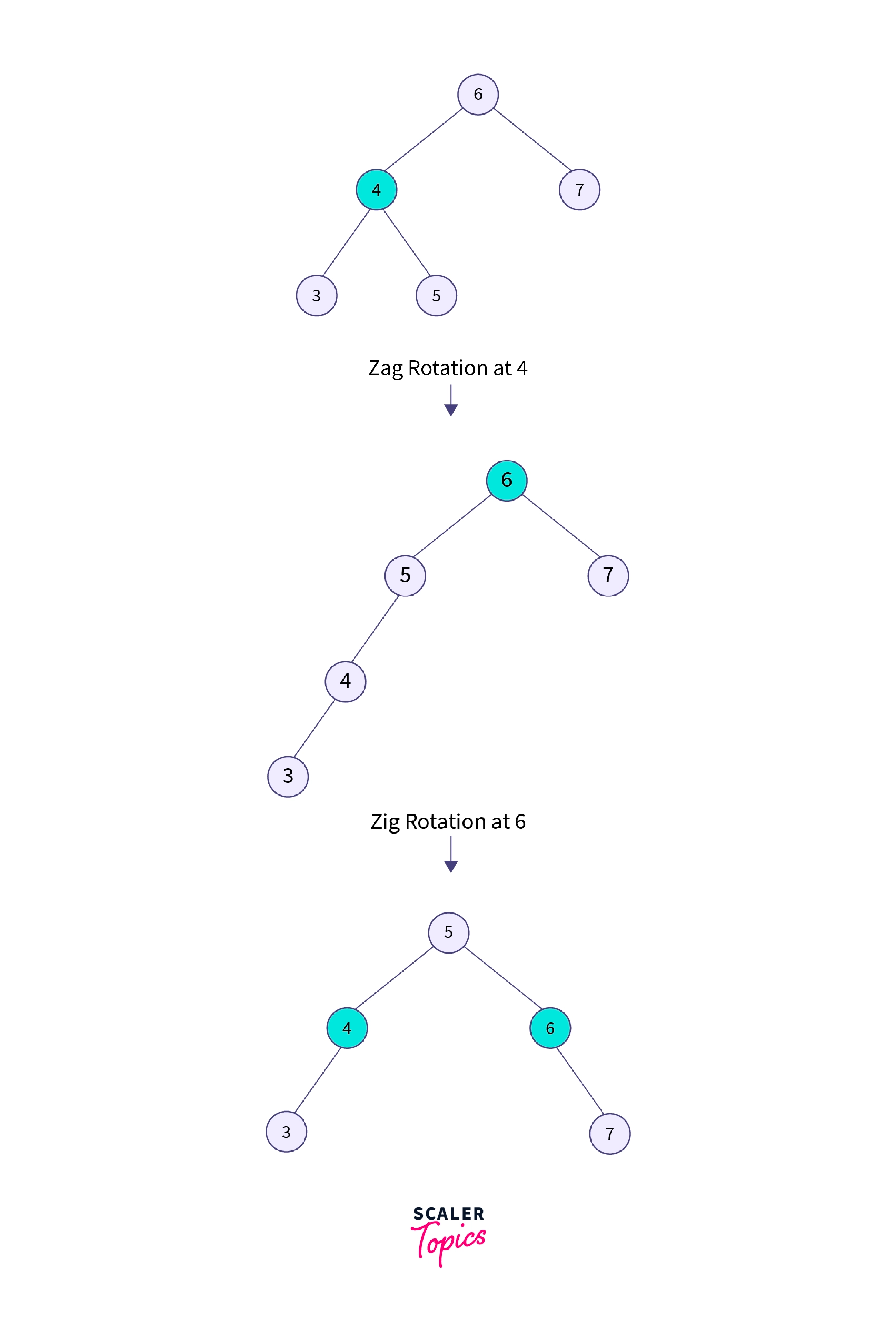
As we can observe in the above tree, node 5 has become the root node; therefore, the searching is completed. In this case, first, we have performed the zag rotation and then the zig rotation. So it is known as zag-zig rotation.
Advantages of Splay Tree
- In the AVL and Red-Black trees, we need to store some information. Like in AVL trees, we need to store the balance factor of each node, and in the red-black trees, we also need to store one extra bit of information that denotes the color of the node, either black or red.
- Splay tree is the fastest type of binary search tree, which is used in a variety of practical applications such as
GCC compilers. - Improve searching by moving frequently accessed nodes closer to the root node. One of the practical uses is cache implementation, in which recently used data is saved in the cache so that we can access the data more quickly without going into memory.
Disadvantages of Splay Tree
The main disadvantage of the splay tree is that trees are not strictly balanced, but rather roughly balanced. When the splay trees are linear, the time complexity is O(n).
Implementation of Splay Tree
C
#include <stdio.h>
#include <stdlib.h>
// Tree Node
struct node
{
int key;
struct node *left, *right;
};
// Allocates a new node with the given key and NULL left and right pointers.
struct node *TreeNode(int key)
{
struct node *node = (struct node *)malloc(sizeof(struct node));
node->key = key;
node->left = node->right = NULL;
return (node);
}
// A utility function for right-rotating a y-rooted subtree.
struct node *rightRotate(struct node *x)
{
struct node *y = x->left;
x->left = y->right;
y->right = x;
return y;
}
// A utility function for right-rotating a x-rooted subtree.
struct node *leftRotate(struct node *x)
{
struct node *y = x->right;
x->right = y->left;
y->left = x;
return y;
}
// If the key is present in the tree, this function moves it to the root.
// If the key is not present, it returns the last item accessed by root.
// This function modifies the tree and returns the modified root.
struct node *splay(struct node *root, int key)
{
// Root is NULL or key is present at root.
if (root == NULL || root->key == key)
return root;
// Key lies in left subtree!
if (root->key > key)
{
if (root->left == NULL)
return root;
// Zig-Zig (Left Left)
if (root->left->key > key)
{
// First, recursively bring the key as the root of left-left.
root->left->left = splay(root->left->left, key);
// Do the first rotation for the root, followed by the second rotation.
root = rightRotate(root);
}
else if (root->left->key < key) // Zig-Zag (Left Right)
{
// First, recursively bring the key as the root of left-right.
root->left->right = splay(root->left->right, key);
// Do first rotation for root->left
if (root->left->right != NULL)
root->left = leftRotate(root->left);
}
// Do second rotation for root
return (root->left == NULL) ? root : rightRotate(root);
}
// Key lies in right subtree
else
{
if (root->right == NULL)
return root;
// Zag-Zig (Right Left)
if (root->right->key > key)
{
// Bring the key as root of right-left
root->right->left = splay(root->right->left, key);
// Do first rotation for root->right
if (root->right->left != NULL)
root->right = rightRotate(root->right);
}
// Zag-Zag (Right Right)
else if (root->right->key < key)
{
// Bring the key as root of right-right and do first rotation
root->right->right = splay(root->right->right, key);
root = leftRotate(root);
}
// Do second rotation for root
return (root->right == NULL) ? root : leftRotate(root);
}
}
// The search function for Splay Tree. Note that this function returns the new root of the splay-tree.
// If a key is present in the tree, then it is moved to the root.
struct node *bstSearch(struct node *root, int key)
{
return splay(root, key);
}
// A utility function to print preorder traversal of the tree.
void preOrder(struct node *root)
{
if (root != NULL)
{
printf("%d ", root->key);
preOrder(root->left);
preOrder(root->right);
}
}
// main function
int main()
{
struct node *root = TreeNode(100);
root->left = TreeNode(50);
root->right = TreeNode(200);
root->left->left = TreeNode(40);
root->left->left->left = TreeNode(30);
root->left->left->left->left = TreeNode(20);
root = bstSearch(root, 20);
preOrder(root);
return 0;
}C++
#include <bits/stdc++.h>
using namespace std;
// Tree Node
class node
{
public:
int key;
node *left, *right;
};
// Allocate a new node with the given key and NULL left and right pointers.
node *TreeNode(int key)
{
node *Node = new node();
Node->key = key;
Node->left = Node->right = NULL;
return (Node);
}
// A utility function for right-rotating a y-rooted subtree.
node *rightRotate(node *x)
{
node *y = x->left;
x->left = y->right;
y->right = x;
return y;
}
// A utility function for right-rotating a x-rooted subtree.
node *leftRotate(node *x)
{
node *y = x->right;
x->right = y->left;
y->left = x;
return y;
}
// If the key is present in the tree, this function moves it to the root.
// If the key is not present, it returns the last item accessed by root.
// This function modifies the tree and returns the modified root.
node *splay(node *root, int key)
{
// Root is NULL or key is present at root.
if (root == NULL || root->key == key)
return root;
// Key lies in left subtree!
if (root->key > key)
{
// Key is not in tree, we are done
if (root->left == NULL)
return root;
// Zig-Zig (Left Left)
if (root->left->key > key)
{
// First, recursively bring the key as the root of left-left.
root->left->left = splay(root->left->left, key);
// Do the first rotation for the root, followed by the second rotation.
root = rightRotate(root);
}
else if (root->left->key < key) // Zig-Zag (Left Right)
{
// First, recursively bring the key as the root of left-right.
root->left->right = splay(root->left->right, key);
// Do first rotation for root->left
if (root->left->right != NULL)
root->left = leftRotate(root->left);
}
// Do second rotation for root
return (root->left == NULL) ? root : rightRotate(root);
}
// Key lies in right subtree
else
{
if (root->right == NULL)
return root;
// Zag-Zig (Right Left)
if (root->right->key > key)
{
// Bring the key as root of right-left
root->right->left = splay(root->right->left, key);
// Do first rotation for root->right
if (root->right->left != NULL)
root->right = rightRotate(root->right);
}
// Zag-Zag (Right Right)
else if (root->right->key < key)
{
// Bring the key as root of right-right and do first rotation
root->right->right = splay(root->right->right, key);
root = leftRotate(root);
}
// Do second rotation for root
return (root->right == NULL) ? root : leftRotate(root);
}
}
// The search function for Splay Tree. Note that this function returns the new root of the splay-tree.
// If a key is present in the tree, then it is moved to the root.
node *bstSearch(node *root, int key)
{
return splay(root, key);
}
// A utility function to print preorder traversal of the tree.
void preOrder(node *root)
{
if (root != NULL)
{
cout << root->key << " ";
preOrder(root->left);
preOrder(root->right);
}
}
// Driver Code
int main()
{
node *root = TreeNode(100);
root->left = TreeNode(50);
root->right = TreeNode(200);
root->left->left = TreeNode(40);
root->left->left->left = TreeNode(30);
root->left->left->left->left = TreeNode(20);
root = bstSearch(root, 20);
preOrder(root);
return 0;
}Java
class Main{
// Tree Node
static class node
{
int key;
node left, right;
};
// Allocates a new node with the given key and NULL left and right pointers.
static node TreeNode(int key)
{
node Node = new node();
Node.key = key;
Node.left = Node.right = null;
return (Node);
}
// A utility function for right-rotating a y-rooted subtree.
static node rightRotate(node x)
{
node y = x.left;
x.left = y.right;
y.right = x;
return y;
}
// A utility function for right-rotating a x-rooted subtree.
static node leftRotate(node x)
{
node y = x.right;
x.right = y.left;
y.left = x;
return y;
}
// If the key is present in the tree, this function moves it to the root.
// If the key is not present, it returns the last item accessed by root.
// This function modifies the tree and returns the modified root.
static node splay(node root, int key)
{
// Root is NULL or key is present at root.
if (root == null || root.key == key)
return root;
// Key lies in left subtree!
if (root.key > key)
{
if (root.left == null) return root;
// Zig-Zig (Left Left)
if (root.left.key > key)
{
// First, recursively bring the key as the root of left-left.
root.left.left = splay(root.left.left, key);
// Do the first rotation for the root, followed by the second rotation.
root = rightRotate(root);
}
// Zig-Zag (Left Right)
else if (root.left.key < key)
{
// First, recursively bring the key as the root of left-right.
root.left.right = splay(root.left.right, key);
// Do first rotation for root->left
if (root.left.right != null)
root.left = leftRotate(root.left);
}
// Do second rotation for root
return (root.left == null) ? root : rightRotate(root);
}
// Key lies in right subtree
else
{
if (root.right == null) return root;
// Zag-Zig (Right Left)
if (root.right.key > key)
{
// Bring the key as root of right-left
root.right.left = splay(root.right.left, key);
// Do first rotation for root->right
if (root.right.left != null)
root.right = rightRotate(root.right);
}
// Zag-Zag (Right Right)
else if (root.right.key < key)
{
// Bring the key as root of right-right and do first rotation
root.right.right = splay(root.right.right, key);
root = leftRotate(root);
}
// Do second rotation for root
return (root.right == null) ? root : leftRotate(root);
}
}
// The search function for Splay Tree. Note that this function returns the new root of the splay-tree.
// If a key is present in the tree, then it is moved to the root.
static node bstSearch(node root, int key)
{
return splay(root, key);
}
// A utility function to print preorder traversal of the tree.
static void preOrder(node root)
{
if (root != null)
{
System.out.print(root.key + " ");
preOrder(root.left);
preOrder(root.right);
}
}
// Driver code
public static void main(String[] args)
{
node root = TreeNode(100);
root.left = TreeNode(50);
root.right = TreeNode(200);
root.left.left = TreeNode(40);
root.left.left.left = TreeNode(30);
root.left.left.left.left = TreeNode(20);
root = bstSearch(root, 20);
preOrder(root);
}
}Python
class TreeNode:
def __init__(self, data):
self.data = data
self.parent = None
self.left = None
self.right = None
class SplayTree:
def __init__(self):
self.root = None
def leftRotate(self, x):
y = x.right
x.right = y.left
if y.left != None:
y.left.parent = x
y.parent = x.parent
# x is root
if x.parent == None:
self.root = y
# x is left child
elif x == x.parent.left:
x.parent.left = y
# x is right child
else:
x.parent.right = y
y.left = x
x.parent = y
def rightRotate(self, x):
y = x.left
x.left = y.right
if y.right != None:
y.right.parent = x
y.parent = x.parent
# x is root
if x.parent == None:
self.root = y
# x is right child
elif x == x.parent.right:
x.parent.right = y
# x is left child
else:
x.parent.left = y
y.right = x
x.parent = y
def splay(self, n):
# node is not root
while n.parent != None:
# node is child of root, one rotation
if n.parent == self.root:
if n == n.parent.left:
self.rightRotate(n.parent)
else:
self.leftRotate(n.parent)
else:
p = n.parent
g = p.parent # grandparent
if n.parent.left == n and p.parent.left == p: # both are left children
self.rightRotate(g)
self.rightRotate(p)
elif n.parent.right == n and p.parent.right == p: # both are right children
self.leftRotate(g)
self.leftRotate(p)
elif n.parent.right == n and p.parent.left == p:
self.leftRotate(p)
self.rightRotate(g)
elif n.parent.left == n and p.parent.right == p:
self.rightRotate(p)
self.leftRotate(g)
def insert(self, n):
y = None
temp = self.root
while temp != None:
y = temp
if n.data < temp.data:
temp = temp.left
else:
temp = temp.right
n.parent = y
if y == None: # newly added node is root
self.root = n
elif n.data < y.data:
y.left = n
else:
y.right = n
self.splay(n)
def bstSearch(self, n, x):
if x == n.data:
self.splay(n)
return n
elif x < n.data:
return self.bstSearch(n.left, x)
elif x > n.data:
return self.bstSearch(n.right, x)
else:
return None
def inOrder(self, n):
if n != None:
self.inOrder(n.left)
print(n.data, end=' ')
self.inOrder(n.right)
if __name__ == '__main__':
tree = SplayTree()
a = TreeNode(10)
b = TreeNode(20)
c = TreeNode(30)
d = TreeNode(100)
e = TreeNode(90)
f = TreeNode(40)
g = TreeNode(50)
tree.insert(a)
tree.insert(b)
tree.insert(c)
tree.insert(d)
tree.insert(e)
tree.insert(f)
tree.insert(g)
tree.bstSearch(tree.root, 90)
tree.inOrder(tree.root)
print()Ignite Data Structures Brilliance! Enroll in Scaler Academy’s Online DSA Course to Hone Your Coding Skills.
Conclusion
- Splay Tree in data structures is a type of binary search tree that uses a splaying operation on the tree so the most frequently used elements can come closer to the root.
- Splay tree is the fastest type of binary search tree, which is used in a variety of practical applications such as GCC compilers.
