Problem Statement
You have a collection of non-negative values, representing available options, and a non-negative target value. Your task is to determine whether there exists a subset within the collection whose sum equals the given target value.
Example
Example1:
Input: arr = [1, 2, 3], target_sum = 3
Output: True
Explanation: There is a subset (1, 2) with sum 3.
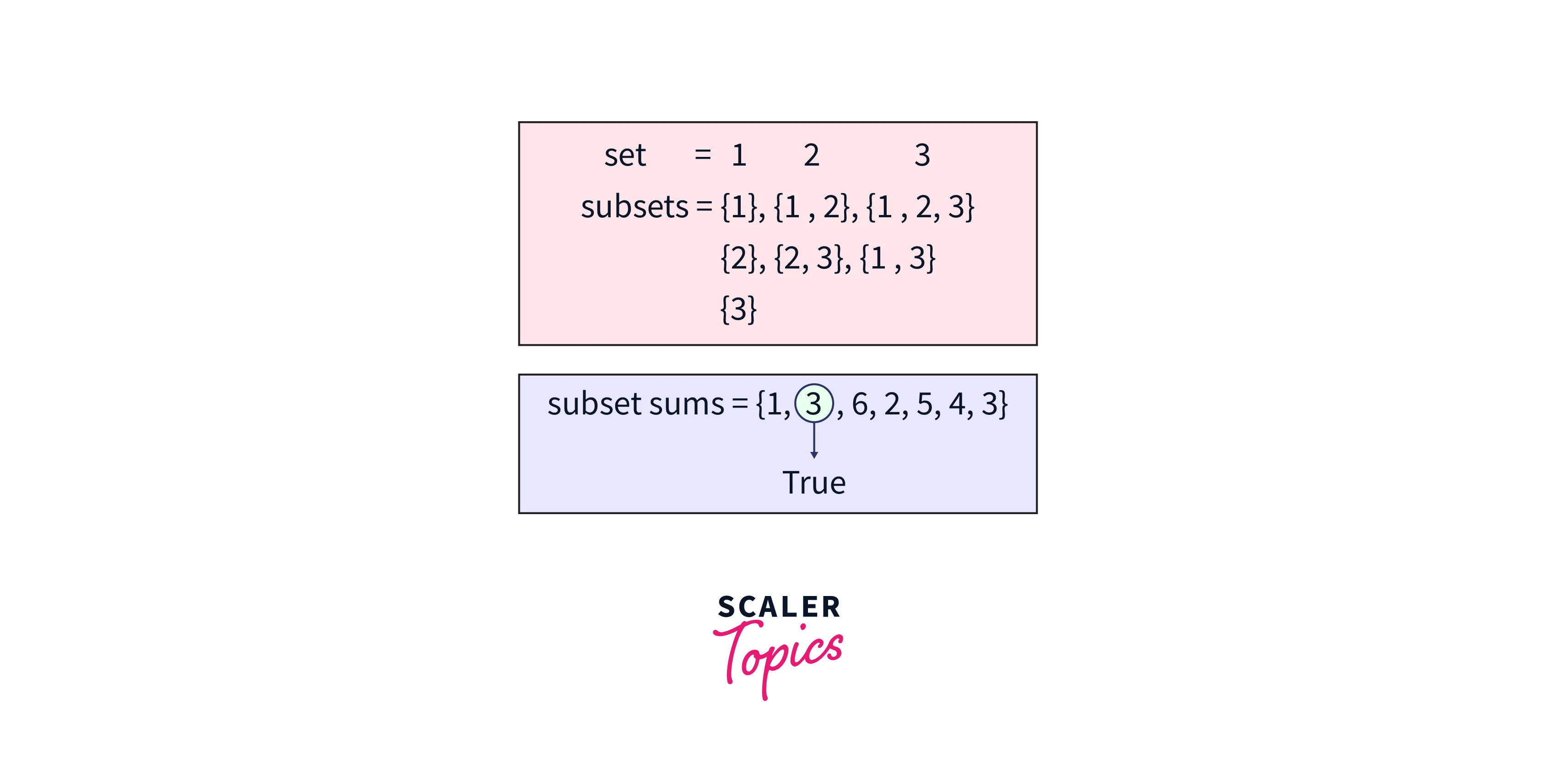
Example2:
Input: arr = {10, 20, 30, 40, 50}, sum = 25
Output: False
Explanation: There is no subset whose sum will be equal to 25.
Approach 1: Using Recursion
We can approach the Subset Sum Problem recursively by considering two cases for each element in the set:
- Case 1: Include the current element in the subset. In this case, reduce the target sum by the value of the current element, and consider the remaining elements in the set.
- Case 2: Exclude the current element from the subset. In this case, keep the target sum unchanged and consider the remaining elements in the set.
The recursion continues until we either find a subset that satisfies the target sum or exhaust all elements in the set.
Following is the recursion tree:
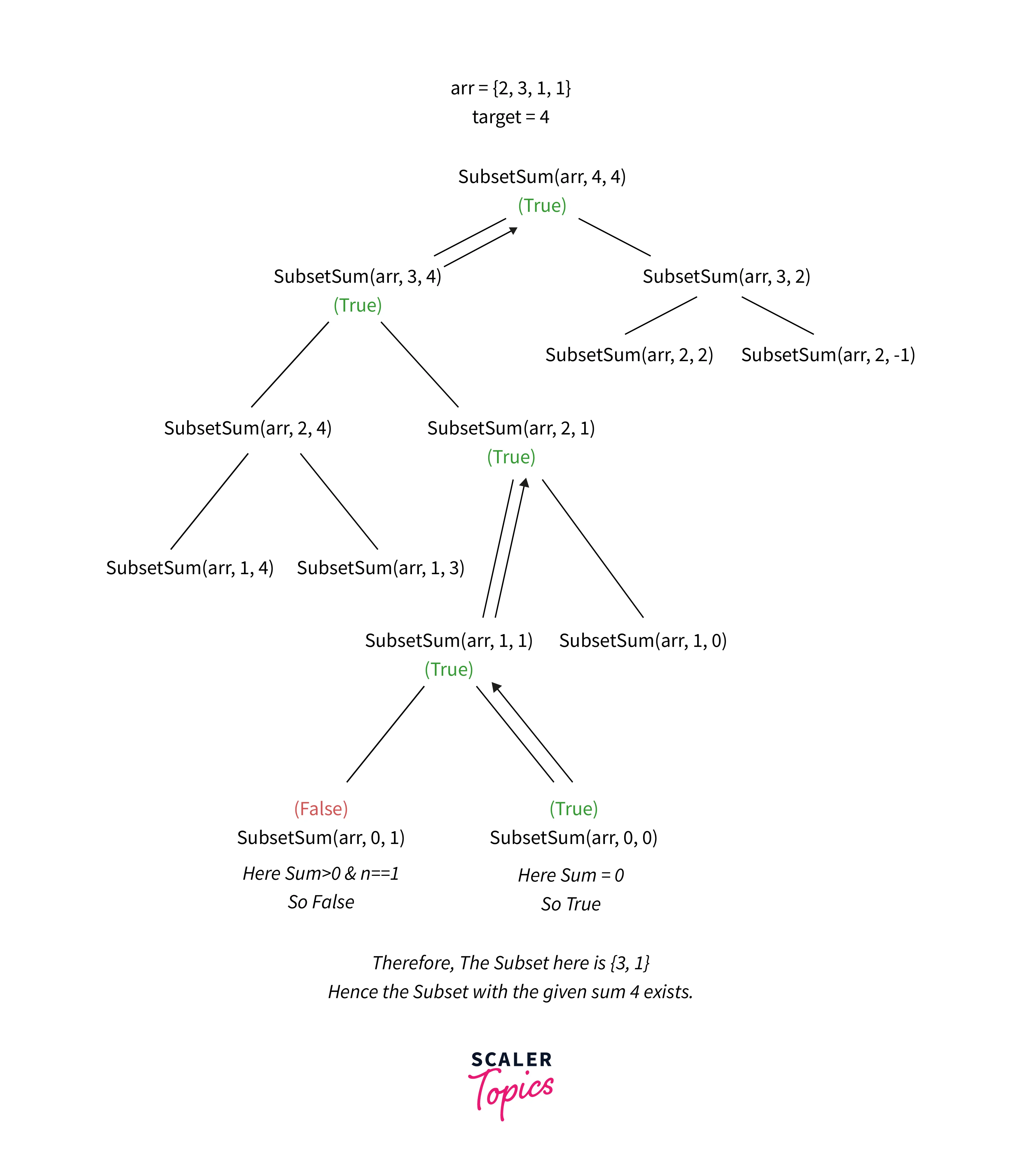
Algorithm:
- Define a recursive function that takes the current index of the set and the remaining sum to be achieved.
- For each index, check the base cases:
- If the remaining sum is zero, return true (subset found).
- If there are no elements left to consider (index becomes zero) and the remaining sum is still positive, return false (no subset found).
- Recur by considering two cases:
- Case 1: Include the current element and reduce the remaining sum by the value of the current element.
- Case 2: Exclude the current element and keep the remaining sum unchanged.
- If any of the recursive calls return true, then there exists a subset that satisfies the target sum; otherwise, no such subset exists.
Code Implementation
C++
// C++ implementation of subset sum using recursion
#include <iostream>
using namespace std;
// This recursive function returns true if there exists a sum, else false
bool SubsetSum(int set_1[], int N, int target_sum){
// Base Case 1 if target sum reaches 0, we have found a subset sum equal to targetsum
if (target_sum == 0)
return true;
// Base Case 2, if we reach the 0 index without finding the subset sum
if (N == 0)
return false;
// if we find a element larger then the target we just don't include it in the subset
if (set_1[N - 1] > target_sum)
return SubsetSum(set_1, N - 1, target_sum);
// if the number is not greater than target_sum we call the both recurrance relations
// if any of the below gives true, we have found the case.
return SubsetSum(set_1, N - 1, target_sum) || SubsetSum(set_1, N - 1, target_sum - set_1[N - 1]);
}
// Driver code
int main(){
// given set of elements are:
int set_1[] = {2, 3, 1, 1};
// given target sum is :
int target_sum = 4;
// length of the set array
int N = sizeof(set_1) / sizeof(set_1[0]);
// Calling the SubsetSum to check whether subset sum equals target sum in the given set of elements
if (SubsetSum(set_1, N, target_sum))
// if exists return true
cout <<"True";
else
// if not return false
cout <<"False";
return 0;
}
Python
# Python implementation of subset-sum using recursion
# this recursive function returns true if there exists a sum, else false
def SubsetSum(set_1, N, target_sum):
# Base Case 1 if target sum reaches 0, we have found a subset sum equal to targetsum
if (target_sum == 0):
return True
# Base Case 2, if we reach the 0 index without finding the subset sum
if (N == 0):
return False
# if we find a element larger then the target we just don't include it in the subset
if (set_1[N - 1] > target_sum):
# we recurr without changing the sum and decrementing the index
return SubsetSum(set_1, N - 1, target_sum)
# if the number is not greater than target_sum we call the both recurrance relations
# if any of the below gives true, we have found the case.
return SubsetSum(set_1, N-1, target_sum) or SubsetSum(set_1, N-1, target_sum-set_1[N-1])
# Driver code
# given set of elements are:
set_1 = [2, 3, 1, 1]
# given target sum is :
target_sum = 4
# length of the set array
N = len(set_1)
# Calling the SubsetSum to check whether subset sum equals target sum in the given set of elements
if (SubsetSum(set_1, N, target_sum)):
# if exists return true
print("True")
else:
# return False
print("False")
Java
// Java implementation of subset-sum using recursion
class Solution {
// This recursive function returns true if there exists a sum, else false
static boolean SubsetSum(int set_1[], int N, int target_sum){
// Base Case 1 if target sum reaches 0, we have found a subset sum equal to targetsum
if (target_sum == 0)
return true;
// Base Case 2, if we reach the 0 index without finding the subset sum
if (N == 0)
return false;
// if we find a element larger then the target we just don't include it in the subset
if (set_1[N - 1] > target_sum)
// we recurr without changing the sum and decrementing the index
return SubsetSum(set_1, N - 1, target_sum);
// if the number is not greater than target_sum we call the both recurrance relations
// if any of the below gives true, we have found the case.
return SubsetSum(set_1, N - 1, target_sum) || SubsetSum(set_1, N - 1, target_sum - set_1[N - 1]);
}
// Driver code
public static void main(String args[]){
// given set of elements are:
int set_1[] = {2, 3, 1, 1};
// given target sum is :
int target_sum = 4;
// length of the set array
int N = set_1.length;
// Calling the SubsetSum to check whether subset sum equals target sum in the given set of elements
if (SubsetSum(set_1, N, target_sum))
// if exists return true
System.out.println("True");
else
// if not return false
System.out.println("False");
}
}
Output:
True
Complexity Analysis
Time Complexity: The time complexity of recursive solution for the Subset Sum Problem is exponential, O(2^n), as it may need to explore all possible subsets of the given set to find the solution. This problem is classified as NP-Complete, indicating that there is no known polynomial-time solution for it.
Space Complexity: The auxiliary space complexity of the recursive solution is O(n), where n represents the recursion stack space required for the recursive calls.
Approach 2: Using Memoization
- Utilize dynamic programming by creating a 2D array to store the results of subproblems.
- Each state in the solution can be uniquely identified by two variables: the index and the remaining sum.
- Compute and store the value of each state in the 2D array to avoid recalculation of the same state.
By memoizing the results, we can significantly reduce the time complexity of the algorithm, making it more efficient compared to the naive recursive approach.
Code Implementation
C++
// CPP program for subset sum problem using dynamic programming Memoization technique:
#include <bits/stdc++.h>
using namespace std;
// a 2-d dp array taken globally
int dp[1000][1000];
// Check if possible subset with
// given sum is possible or not
int SubsetSum(int arr[], int N, int target_sum)
{
// Base Case 1 if target sum reaches 0, we have found a subset sum equal to targetsum
if (target_sum == 0)
return 1;
// Base Case 2, if we reach the 0 index without finding the subset sum
if (N <= 0)
return 0;
// If the value is not -1 in the dp table, it means that it is already a called the function with the same value. This will save our from the repetition of subcalls again.
if (dp[N - 1][target_sum] != -1)
return dp[N - 1][target_sum];
// if we find a element larger then the target we just don't include it in the subset, we simpley go for next call
if (arr[N - 1] > target_sum)
return dp[N - 1][target_sum] = SubsetSum(arr, N - 1, target_sum);
else{
// if the number is not greater than target_sum we call the both recurrance relations
return dp[N - 1][target_sum] = SubsetSum(arr, N - 1, target_sum) ||
SubsetSum(arr, N - 1, target_sum - arr[N - 1]);
}
}
// Driver Code
int main()
{
// Storing the value -1 to the matrix
// a 2-d dp array where every value is initialised to -1
memset(dp, -1, sizeof(dp));
int N = 5;
// the set of elements
int arr[] = {1, 2, 3};
// given target sum
int target_sum = 3;
if (SubsetSum(arr, N, target_sum)){
cout << "True" << endl;
}
else
cout << "False" << endl;
}
Python
# Python implementation for finding the subset-sum using dynamic programming Memoization technique:
# a 2-d dp array where every value is initialised to -1
dp = [[-1 for i in range(1000)] for j in range(1000)]
# this recursive function returns 1 if there exists a sum, else 0
def SubsetSum(arr, N, target_sum):
# Base Case 1 if target sum reaches 0, we have found a subset sum equal to targetsum
if (target_sum == 0):
return 1
# Base Case 2, if we reach the 0 index without finding the subset sum
if (N <= 0):
return 0
# If the value is not -1 in the dp table, it means that it is already a called the function with the same value. # This will save our from the repetition of subcalls again.
if (dp[N - 1][target_sum] != -1):
return dp[N - 1][target_sum]
# if we find a element larger then the target we just don't include it in the subset, we simpley go for next call
if (arr[N - 1] > target_sum):
dp[N - 1][target_sum] = subsetSum(arr, N - 1, target_sum)
return dp[N - 1][target_sum]
else:
# if the number is not greater than target_sum we call the both recurrance relations
dp[N - 1][target_sum] = SubsetSum(arr, N - 1, target_sum)
return (dp[N - 1][target_sum] or SubsetSum(arr, N - 1, target_sum - arr[N - 1]))
# Driver code
# given set of elements are:
arr = [1, 2, 3]
# length of the set array
N=len(arr)
# given target sum is :
target_sum = 3
# Calling the SubsetSum to check whether subset-sum equals target sum in the given set of elements
if (SubsetSum(arr, N, target_sum)):
print("True")
else:
print("False")
Java
// Java program for finding the subset-sum using dynamic programming Memoization technique:
class Solution {
// this recursive function returns 1 if there exists a sum, else 0
static int SubsetSum(int arr[], int N, int target_sum) {
// a 2-d dp array where every value is initialised to -1
int dp[][] = new int[N + 1][target_sum + 1];
for (int i = 1; i <= N; i++) {
// a dp array initialised all its values to -1
for (int j = 1; j <= target_sum; j++) {
dp[i][j] = -1;
}
}
// Base Case 1 if target sum reaches 0, we have found a subset sum equal to targetsum
if (target_sum == 0)
return 1;
// Base Case 2, if we reach the 0 index without finding the subset sum
if (N <= 0)
return 0;
// If the value is not -1 in the dp table, it means that it is already a called the function with the same value. This will save our from the repetition of subcalls again.
if (dp[N - 1][target_sum] != -1)
return dp[N - 1][target_sum];
// if we find a element larger then the target we just don't include it in the subset, we simpley go for next call
if (arr[N - 1] > target_sum)
return dp[N - 1][target_sum] = SubsetSum(arr, N - 1, target_sum);
else {
// if the number is not greater than target_sum we call the both recurrance relations
if (SubsetSum(arr, N - 1, target_sum) != 0 || SubsetSum(arr, N - 1, target_sum - arr[N - 1]) != 0) {
return dp[N - 1][target_sum] = 1;
}
else
return dp[N - 1][target_sum] = 0;
}
}
// Driver Code
public static void main(String[] args){
// length of the set array
int N = 3;
// given set of elements are:
int arr[] = { 1, 2, 3 };
// given target sum is :
int target_sum = 3;
// Calling the SubsetSum to check whether subset sum equals target sum in the given set of elements
if(SubsetSum(arr, N, target_sum)!=0) {
System.out.println("True");
}
else
System.out.println("False");
}
}
Output:
True
Complexity Analysis
Time Complexity: The time complexity is O(sum * n) because we iterate through each element in the set and for each element, we iterate through the target sum.
Space Complexity: The auxiliary space complexity is also O(sum * n) because of the 2D array used for memoization and the recursion stack space.
Approach 3: Using Dynamic Programming
To solve the sum of subset problem efficiently using dynamic programming:
- Initialization: Create a 2D boolean array of size (n + 1) * (sum + 1), where n is the size of the given array and sum is the target sum. Initialize the array with appropriate base cases.
- Dynamic Programming Iteration:
- Iterate through each element of the set (i) and each possible sum value (j).
- Use the dynamic programming relation:
- If the current element (A[i-1]) is greater than the current sum value (j), copy the value from the previous row: dp[i][j] = dp[i-1][j].
- Otherwise, update dp[i][j] to true if either dp[i-1][j] is true or dp[i-1][j-set[i-1]] is true.
- Result Check: After completing the iteration, check if dp[n][sum] is true. If true, there exists a subset with the target sum.
This approach effectively identifies whether there exists a subset of elements from the given set that sums up to the target sum, accomplishing the task in pseudo-polynomial time.
Example :
set_1 = [1, 2, 3]
target_sum = 3
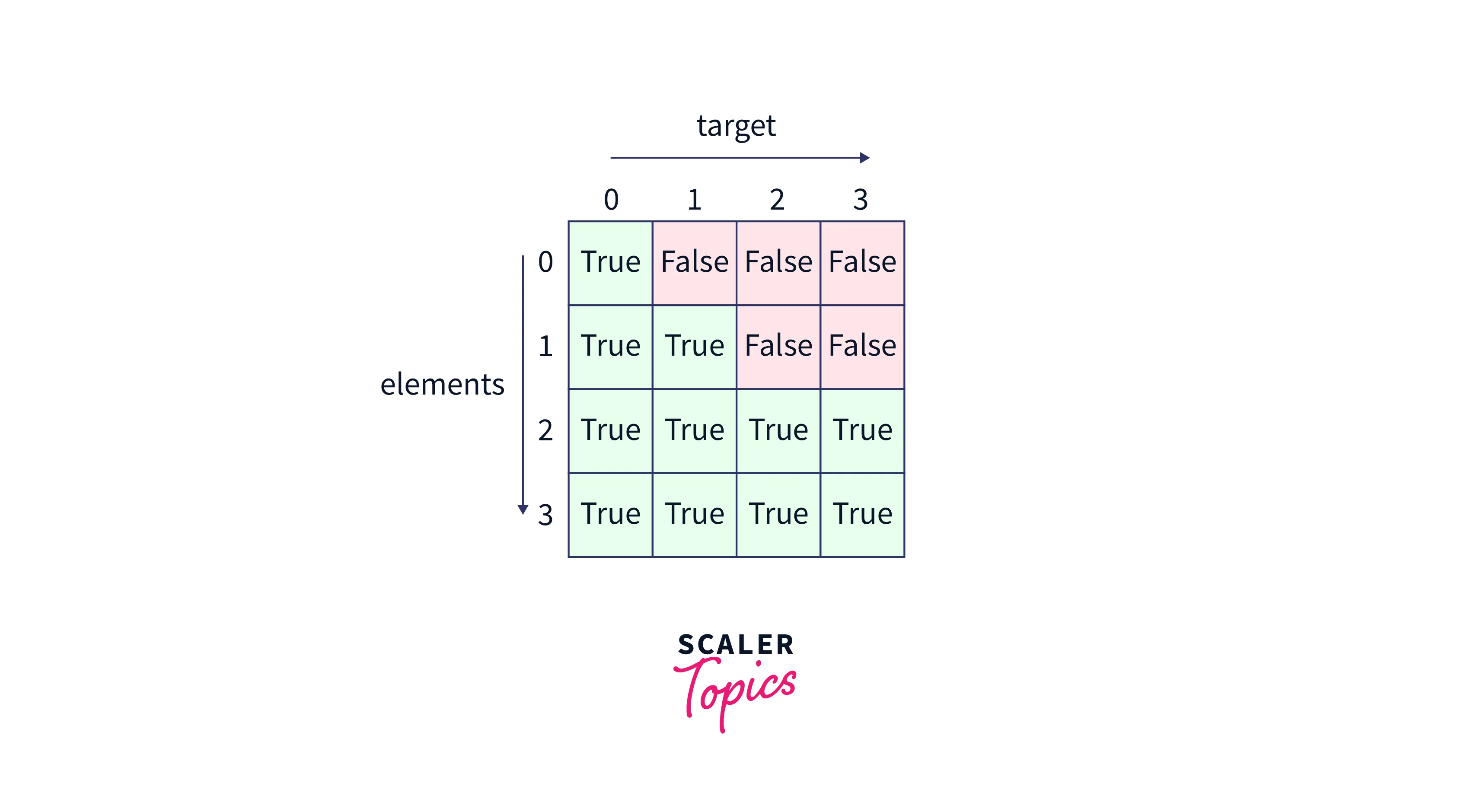
Code Implementation
C++
// cpp implementation program for subset sum using dynamic programming by tabulation method
#include <iostream>
using namespace std;
// this function returns true if there exists a sum, else false
bool SubsetSum(int set_1[], int N, int target_sum)
{
// the value of dp[i][j] is true then there exists a subset sum equals to target_sum
bool dp[N + 1][target_sum + 1];
// If target_sum is 0, then answer is true
for (int i = 0; i <= N; i++)
dp[i][0] = true;
// If target_sum is not 0 and set_1 is empty,
// then answer is false
for (int i = 1; i <= target_sum; i++)
dp[0][i] = false;
// Filling up the dp table in bottom up manner
for (int i = 1; i <= N; i++) {
// row represents each each element
for (int j = 1; j <= target_sum; j++) {
if (j < set_1[i - 1])
// if we find a element larger then the target we just don't include it in the subset
dp[i][j] = dp[i - 1][j];
// if the number is not greater than target_sum we include both the options:
// including it in sub set
// Not including it in subset
if (j >= set_1[i - 1])
dp[i][j] = dp[i - 1][j] || dp[i - 1][j - set_1[i - 1]];
}
}
// the final answer is present at dp[N][target_sum]
return dp[N][target_sum];
}
// Driver Code
int main()
{
// Storing the value -1 to the matrix
int N = 5;
// the set of elements
int arr[] = {1, 2, 3};
// given target sum
int target_sum = 3;
if (SubsetSum(arr, N, target_sum)){
cout << "True" << endl;
}
else
cout << "False" << endl;
}
Python
# python program for subset-sum using dynamic programming by tabulation method
# this function returns true if there exists a sum, else false
def SubsetSum(set_1, N, target_sum):
# The value of dp[i][j] is true then there exists a subset sum equals to target_sum
# initialise this boolean array with false
dp =([[False for i in range(target_sum + 1)] for i in range(N + 1)])
# Base Case 1 if target sum reaches 0, we have found a subset sum equal to targetsum
for i in range(N + 1):
dp[i][0] = True
# Base Case 2, if we reach the 0 index without finding the subset sum return false
for i in range(1, target_sum + 1):
dp[0][i]= False
# Filling up the DP table in bottom up manner
# row represents each letter
for i in range(1, N + 1):
# coloumn represents each target_sum
for j in range(1, target_sum + 1):
# if we find an element larger than the target we don't include it in the subset
if j<set_1[i-1]:
dp[i][j] = dp[i-1][j]
# if the number is not greater than target_sum we include both the options:
# including it in the subset
# Not including it in the subset
if j>= set_1[i-1]:
dp[i][j] = (dp[i-1][j] or dp[i - 1][j-set_1[i-1]])
# the final answer is present at dp[n][sum]
return dp[N][target_sum]
# Driver code
# given set of elements are:
set_1 = [1, 2, 4, 6, 8]
# given target sum is :
target_sum = 9
# length of the set array
N = len(set_1)
# Calling the SubsetSum to check whether subset sum equals target sum in the given set of elements
if (SubsetSum(set_1, N, target_sum)):
# if exists return true
print("True")
else:
# return False
print("False")
Java
// java implementation program for subset-sum using dynamic programming by tabulation method
class Solution {
// this function returns true if there exists a sum, else false
static boolean SubsetSum(int set_1[], int N, int target_sum)
{
// the value of dp[i][j] is true then there exists a subset sum equals to target_sum
boolean dp[][] = new boolean[target_sum + 1][N + 1];
// initialise this boolean array with false
for (int i = 0; i <= N; i++)
dp[0][i] = true;
// If sum is not 0 and set is empty,
// then answer is false
for (int i = 1; i <= target_sum; i++)
dp[i][0] = false;
// Filling up the DP table in bottom up manner
// row represents each target_sum
for (int i = 1; i <= target_sum; i++) {
// row represents each each element
for (int j = 1; j <= N; j++) {
// if we find a element larger then the target we just don't include it in the subset
dp[i][j] = dp[i][j - 1];
// if the number is not greater than target_sum we include both the options:
// including it in sub set
// Not including it in subset
if (i >= set_1[j - 1])
dp[i][j] = dp[i][j] || dp[i - set_1[j - 1]][j - 1];
}
}
// the final answer is present at dp[target_sum][N]
return dp[target_sum][N];
}
// Driver code
public static void main(String args[]){
// given set of elements are:
int set_1[] = {1, 2, 3};
// given target sum is :
int target_sum = 3;
// length of the set array
int N = set_1.length;
// Calling the SubsetSum to check whether subset sum equals target sum in the given set of elements
if (SubsetSum(set_1, N, target_sum))
// if exists return true
System.out.println("True");
else
// if not return false
System.out.println("False");
}
}
Output
True
Complexity Analysis
Time Complexity: O(sum * n) – We iterate through each element in the array and each possible sum value.
Space Complexity: O(sum * n) – The space complexity arises from the 2D array used for dynamic programming, which has a size proportional to the product of the array size and the target sum.
Approach 4: Using Dynamic Programming With Space Optimization to Linear
Instead of storing the entire 2D array for dynamic programming, we only need to store the results for the previous row (prev) and the current row (curr).
Approach:
- Define two arrays: prev and curr, both of size (sum + 1), to store the results of the just previous row and the current row, respectively.
- Iterate through each element in the given array and each possible sum value, updating the curr array based on the dynamic programming relation.
- Once the curr array is calculated, swap it with the prev array to prepare for the next iteration.
- After processing all rows, the answer is stored in the prev array.
By only storing the results for the previous and current rows, we achieve space optimization while still efficiently solving the Subset Sum Problem.
Code Implementation
C++
#include <iostream>
#include <vector>
bool subsetSum(const std::vector<int>& set, int sum) {
int n = set.size();
std::vector<bool> prev(sum + 1, false);
std::vector<bool> curr(sum + 1, false);
prev[0] = true; // Base case: empty subset has sum 0
for (int i = 0; i < n; ++i) {
for (int j = 0; j <= sum; ++j) {
if (j < set[i]) {
curr[j] = prev[j];
} else {
curr[j] = prev[j] || prev[j - set[i]];
}
}
prev = curr; // Update prev array for next iteration
}
return prev[sum];
}
int main() {
std::vector<int> set = {1, 2, 3};
int sum = 3;
if (subsetSum(set, sum)) {
std::cout << "Subset with sum " << sum << " exists.\n";
} else {
std::cout << "No subset with sum " << sum << " exists.\n";
}
return 0;
}
Java
import java.util.Arrays;
public class SubsetSum {
public static boolean subsetSum(int[] set, int sum) {
int n = set.length;
boolean[] prev = new boolean[sum + 1];
boolean[] curr = new boolean[sum + 1];
prev[0] = true; // Base case: empty subset has sum 0
for (int i = 0; i < n; ++i) {
for (int j = 0; j <= sum; ++j) {
if (j < set[i]) {
curr[j] = prev[j];
} else {
curr[j] = prev[j] || prev[j - set[i]];
}
}
prev = Arrays.copyOf(curr, sum + 1); // Update prev array for next iteration
}
return prev[sum];
}
public static void main(String[] args) {
int[] set = {1, 2, 3};
int sum = 3;
if (subsetSum(set, sum)) {
System.out.println("Subset with sum " + sum + " exists.");
} else {
System.out.println("No subset with sum " + sum + " exists.");
}
}
}
Python
def subset_sum(set, target_sum):
n = len(set)
prev = [False] * (target_sum + 1)
curr = [False] * (target_sum + 1)
prev[0] = True # Base case: empty subset has sum 0
for i in range(n):
for j in range(target_sum + 1):
if j < set[i]:
curr[j] = prev[j]
else:
curr[j] = prev[j] or prev[j - set[i]]
prev = curr[:] # Update prev array for next iteration
return prev[target_sum]
# Example usage:
set = [1, 2, 3]
target_sum = 3
if subset_sum(set, target_sum):
print("Subset with sum", target_sum, "exists.")
else:
print("No subset with sum", target_sum, "exists.")
Output:
Subset with sum 9 exists.
Complexity Analysis
Time Complexity: O(sum * n) – We iterate through each element in the array and each possible sum value.
Space Complexity: O(sum) – The space complexity arises from the 1D array used for dynamic programming, which has a size proportional to the target sum plus one.
Conclusion
- Problem Overview: Subset Sum problem involves finding whether a subset of non-negative values equals a given target sum.
- Approaches: Explored recursive, memoization, dynamic programming, and space-optimized dynamic programming methods.
- Recursion: Simple but exponential time complexity.
- Memoization: Reduces time complexity to O(sum * n) but has high space complexity.
- Dynamic Programming: Efficiently solves the problem with time and space complexity of O(sum * n).
- Space-Optimization: Maintains linear space complexity while achieving the same time complexity as dynamic programming.