Types of Trees in Data Structures

A tree represents a hierarchical arrangement of nodes, forming a non-linear data structure. Each node in the tree holds a value and points to its child nodes, creating a branching structure akin to a natural tree. This hierarchical organization facilitates efficient storage and retrieval of data.

Types of Trees in Data Structure According to the Number of Children

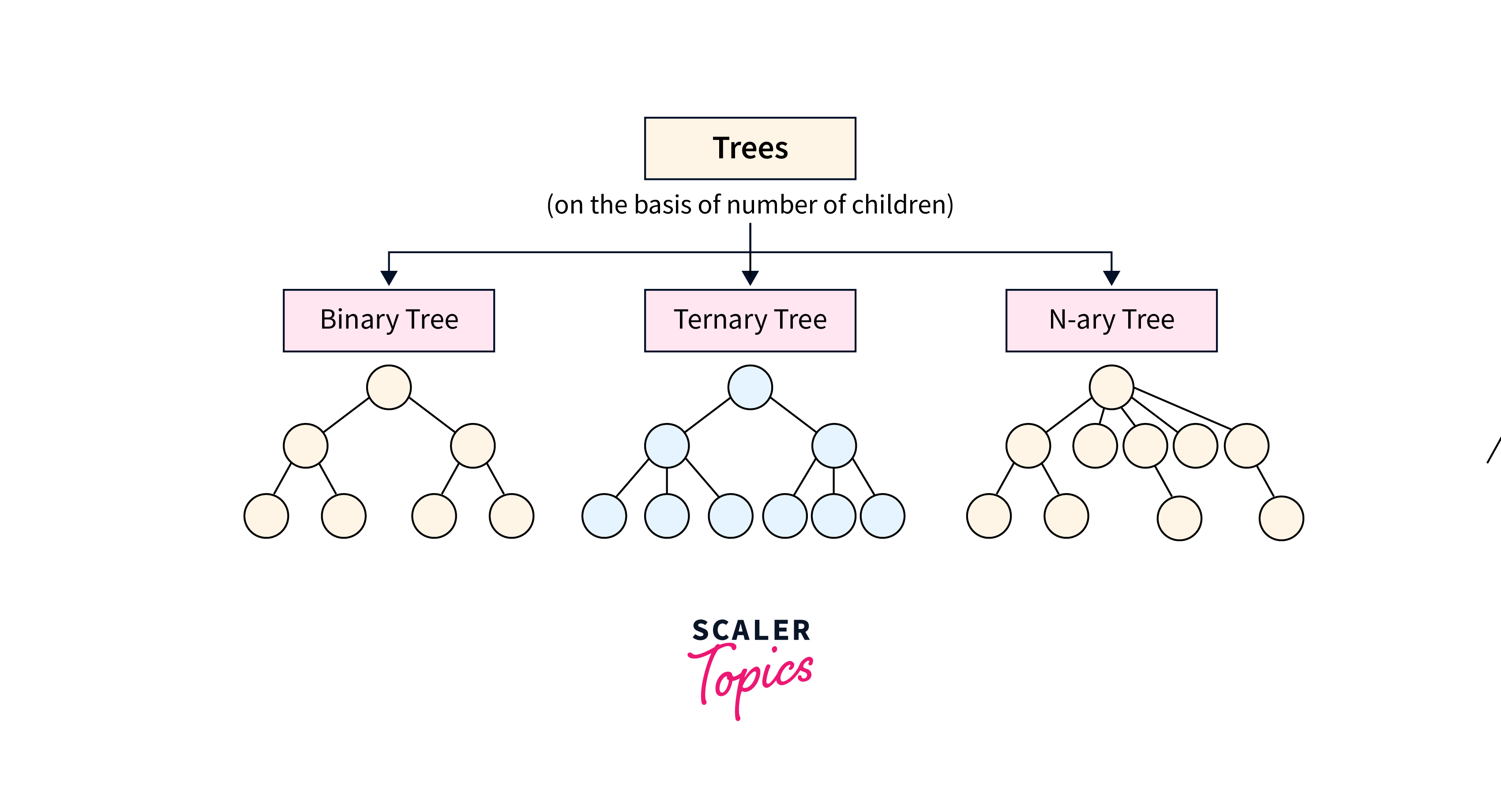
Binary Tree

A binary tree is a type of general tree, except, with a constraint – a node can have only two child nodes. The children nodes are known as the left child node and right child node.

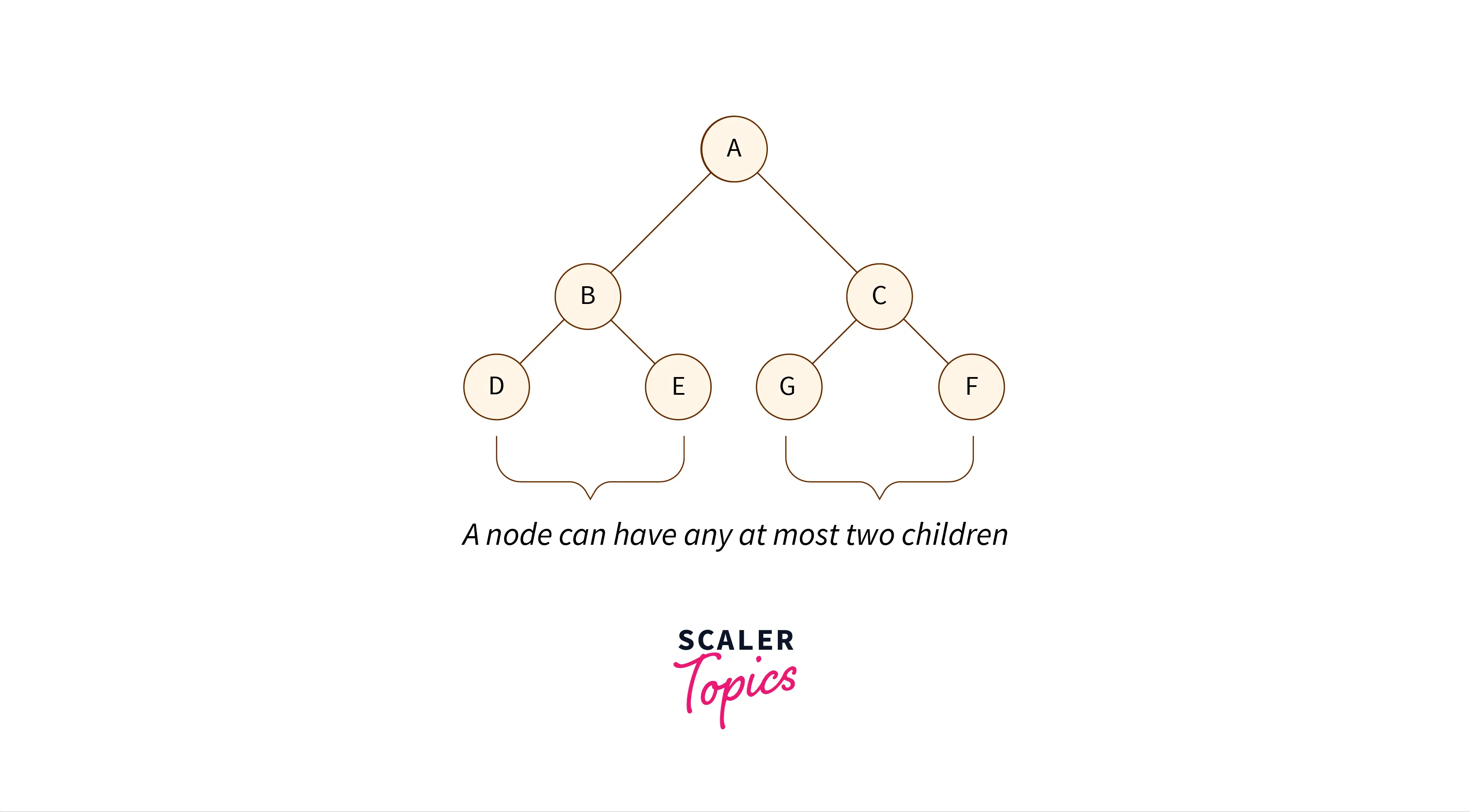
Types of Binary Tree

On the basis of number of children binary tree has two types:

1. Full Binary Tree: All the internal nodes of a full binary tree have two or no child nodes.

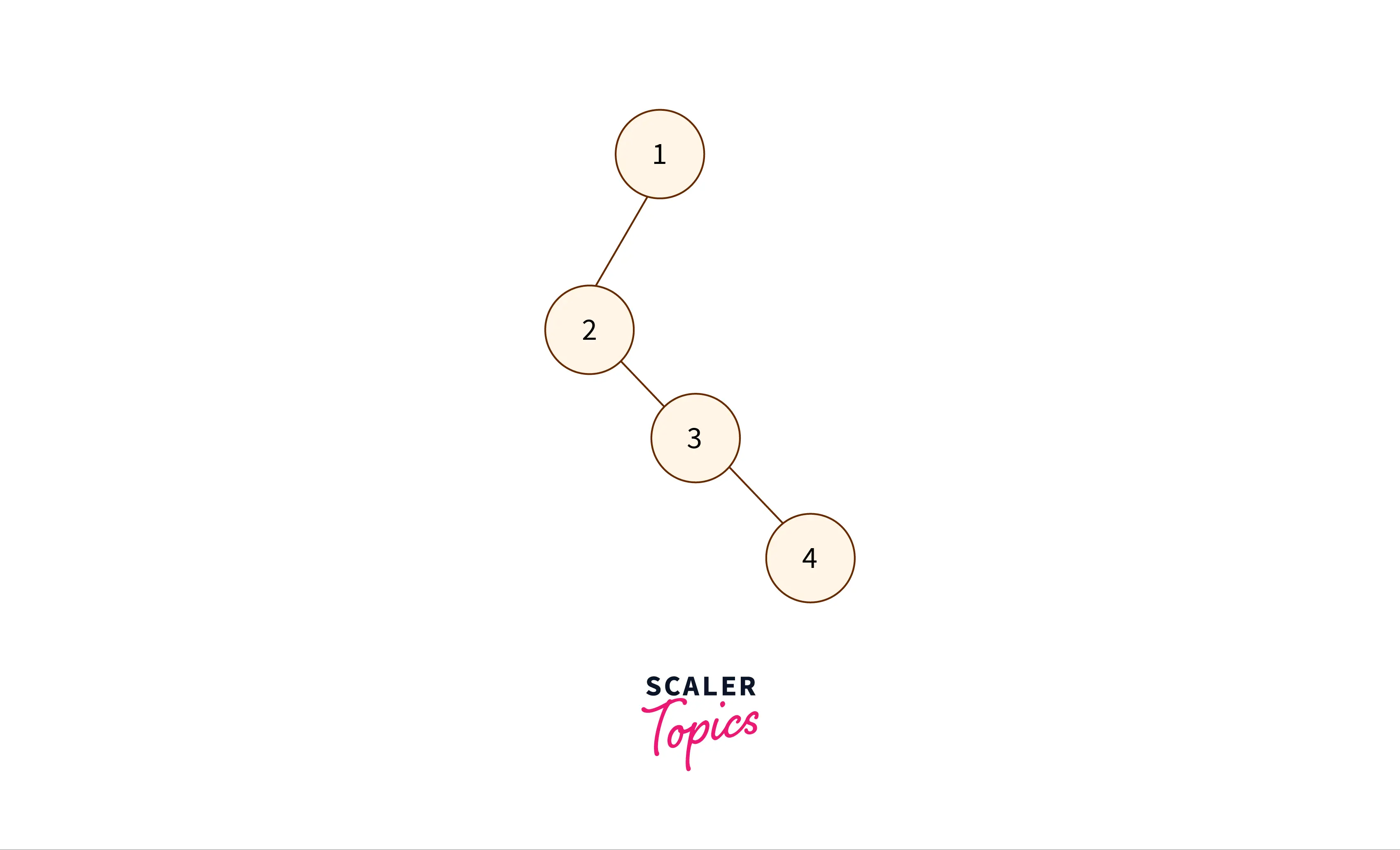
2. Degenerate Binary Tree: Every internal node of the degenerate binary has just one child.

The binary tree can be divided into three types on the basis of completion levels:

1. Perfect Binary Tree: All the leaf nodes of this tree are at the same level. Every internal node of a perfect binary tree has 2 child nodes.

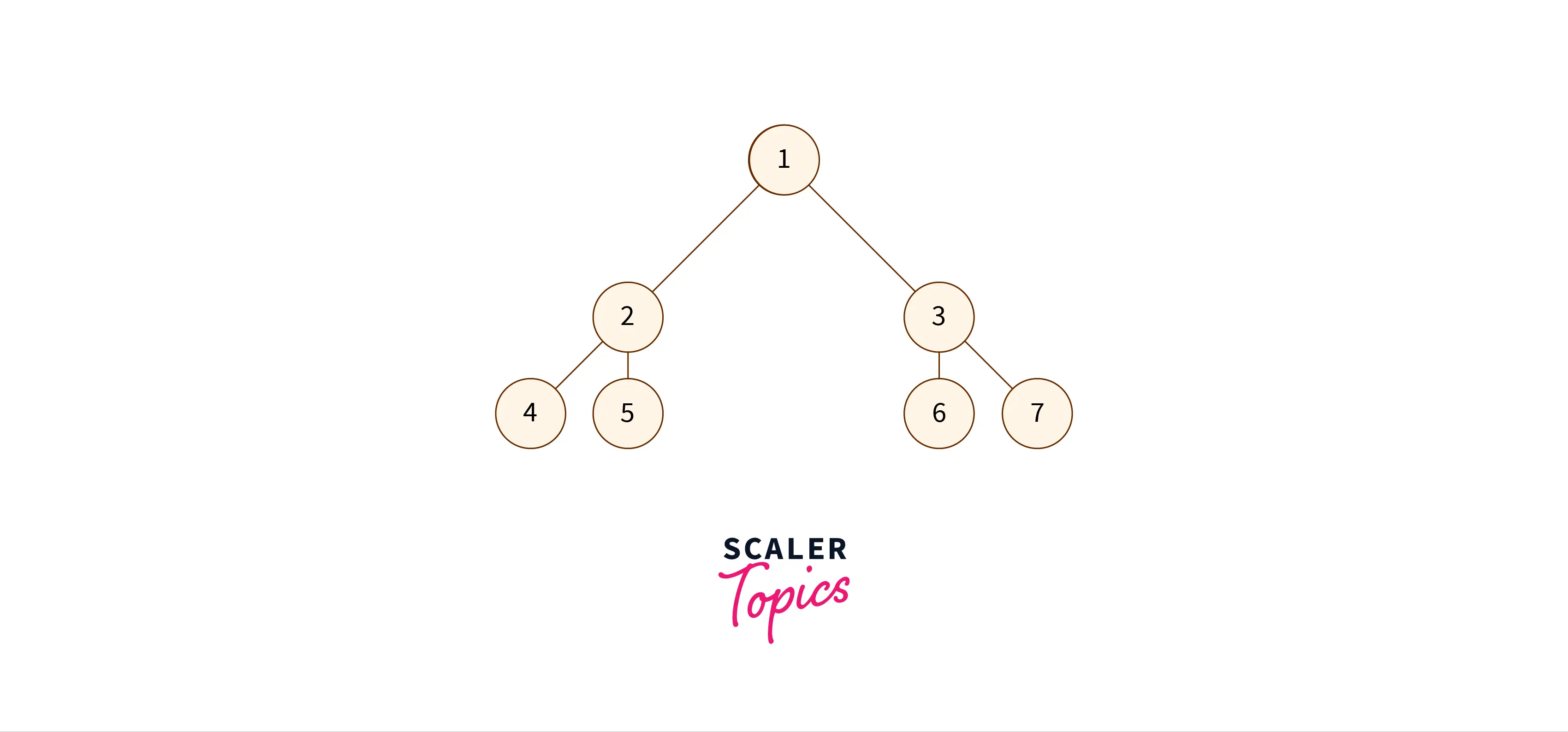
2. Complete Binary Tree: Every level except the last one are full of nodes.

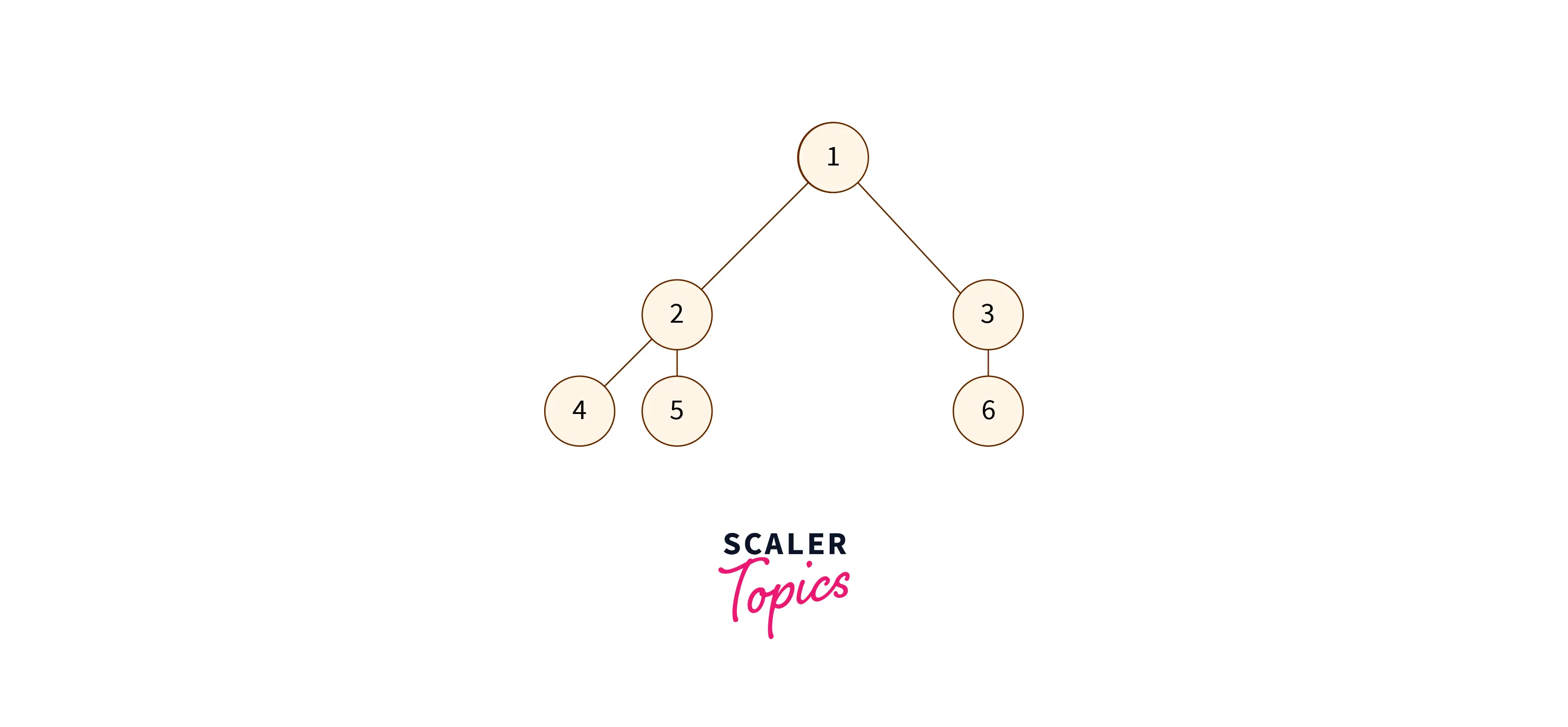
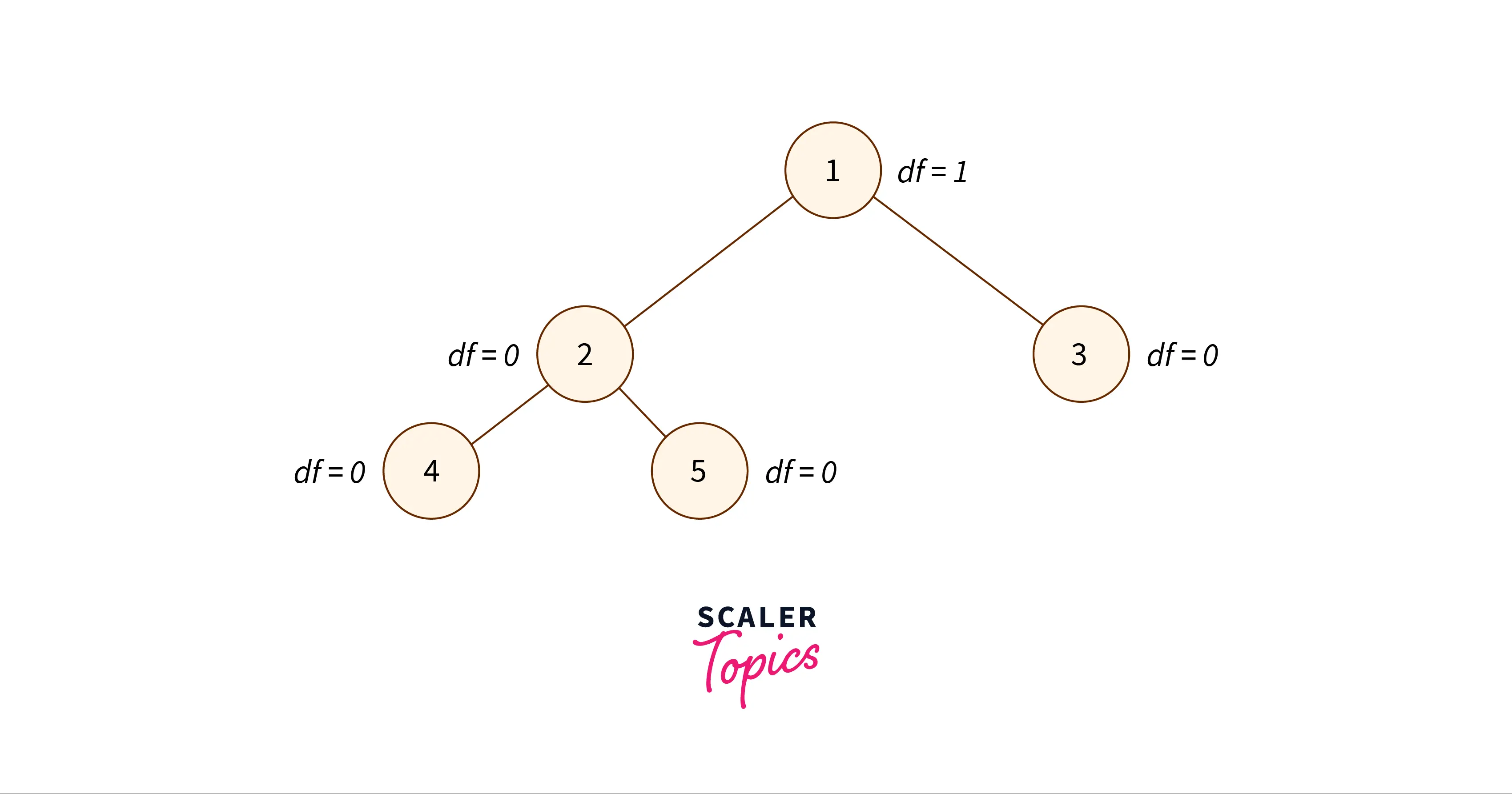
3. Balanced Binary Tree: The difference in height between the left and right subtrees of any node is either 0 or 1.

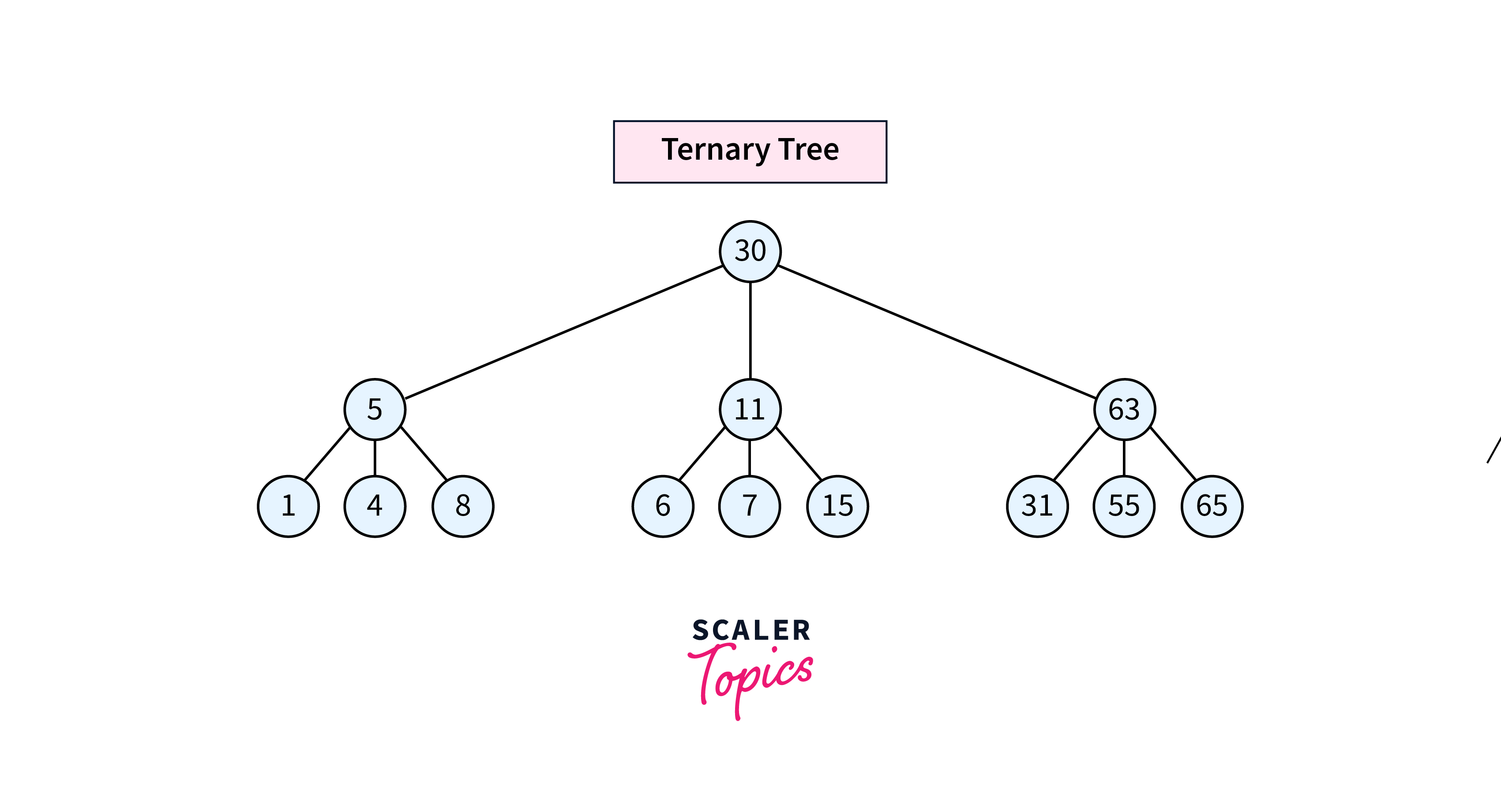
Ternary Tree

It is a type of tree data structure where each node can have a maximum of three child nodes., commonly referred to as “left”, “mid”, and “right”.

Types of Ternary Tree

Ternary Search Tree(TST)

A Ternary Search Tree (TST) is a specialized trie data structure where the child nodes are arranged in the form of a binary search tree.A Ternary Search Tree (TST) node consists of exactly three pointers.

1. The “left” pointer directs to the node with a value smaller than that of the current node.
2. The “equal” pointer directs to the node containing the same value as the current node.
3. The “right” pointer guides to the node with a value greater than that of the current node.

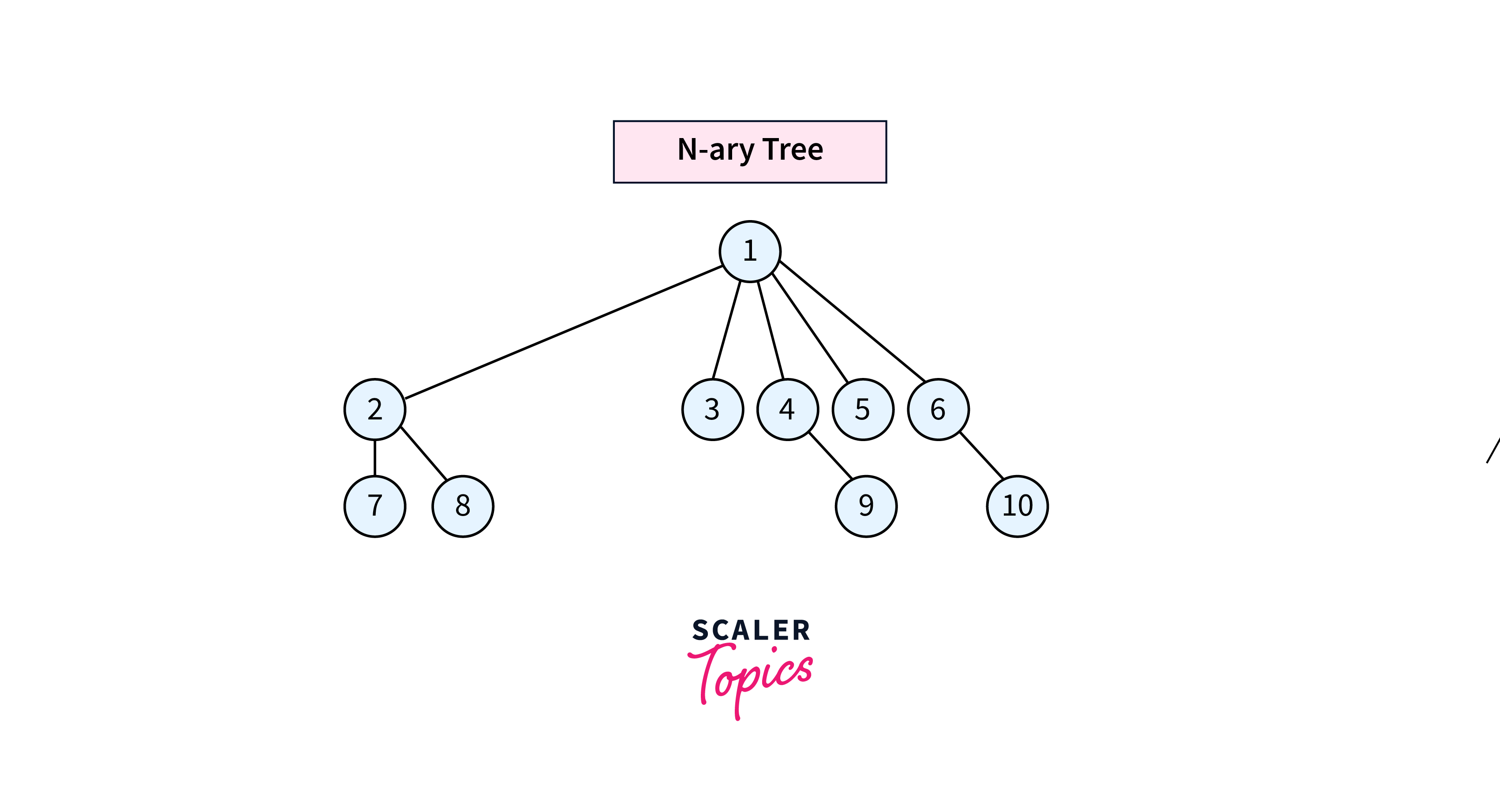
N-ary Tree (Generic Tree)

An N-ary Tree, also called a Generic Tree, is a type of tree data structure. In an N-ary tree, each node holds data records and references to its children. It prohibits duplicate references among its children.

Key features of an N-ary tree:

1. Each node can have multiple children.
2. The exact number of children for each node is not predetermined and may vary.

Types of Trees in Data Structure According to the Nodes Values

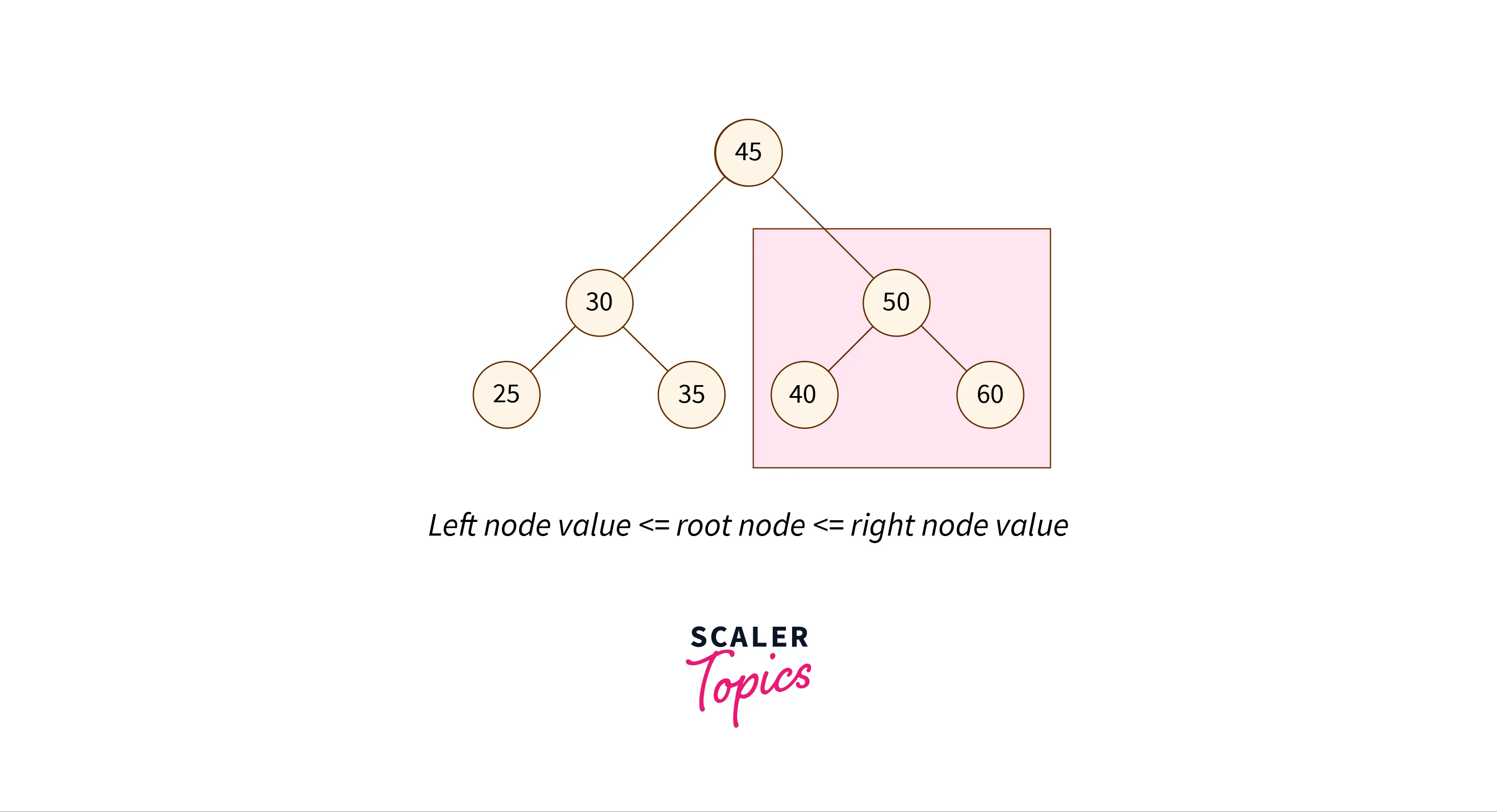
1. Binary Search Tree

A binary search tree shares similarities with a binary tree but has specific limitations.The value of the left child in a binary search tree is always smaller than that of the parent node, and the value of the right child is larger than that of the parent node in the binary search tree. This property makes the binary search tree optimal for search operations.

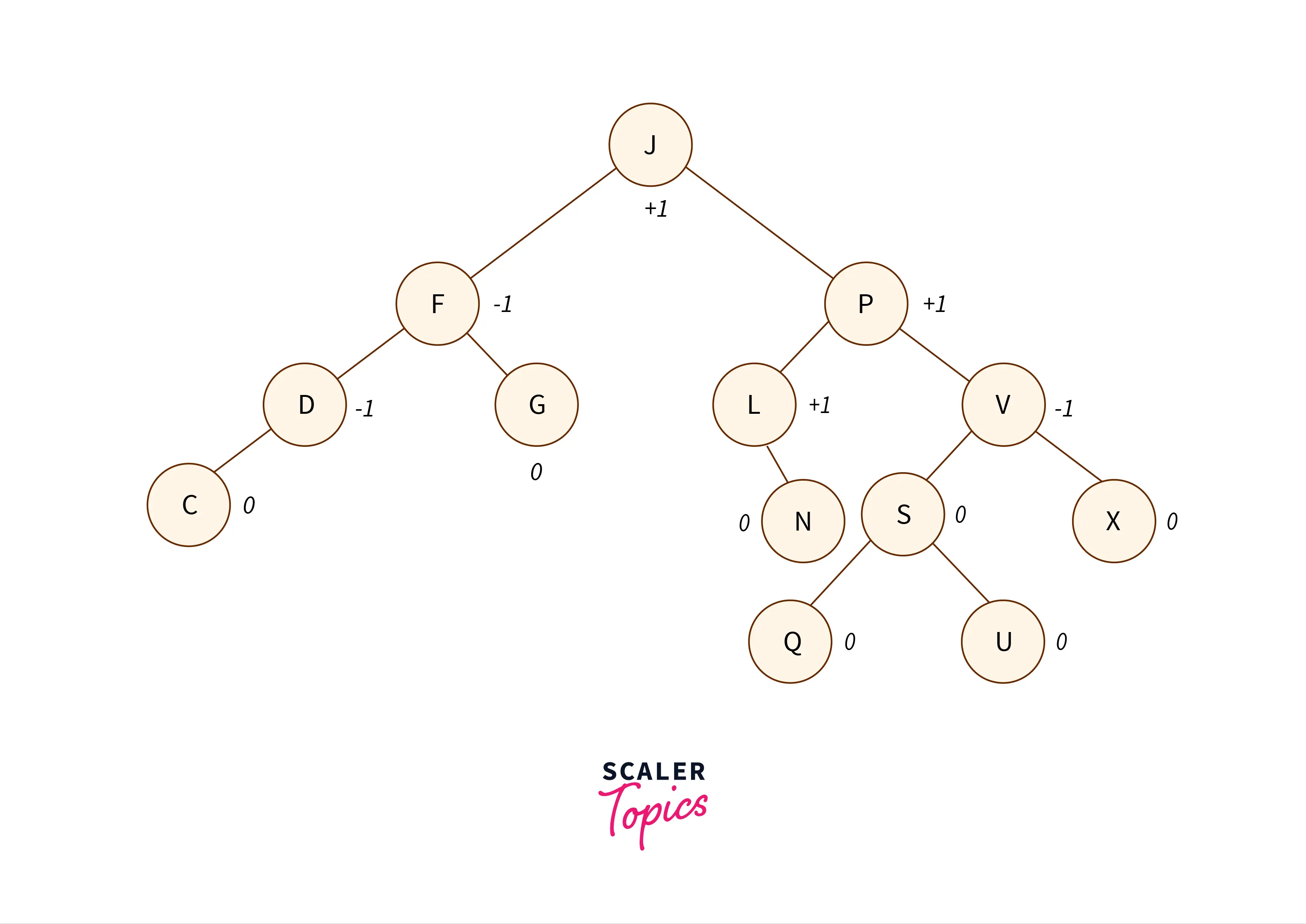
2. AVL Tree

A self-balancing binary search tree is called an AVL tree. In an AVL tree, a balancing factor is given to every node in the tree which depends on whether the tree is balanced or not. These balancing factor values vary between -1, 0, and 1.

• If the right subtree is one level higher than the left subtree of a node, then the balancing factor value of that node is -1.
• If both, the left and right subtrees are at the same level, the balancing factor value is given as 0.
• If the left subtree is one level higher than the right subtree then the balancing factor is 1.

To learn more about the AVL tree, refer to the scaler blog on AVL tree.

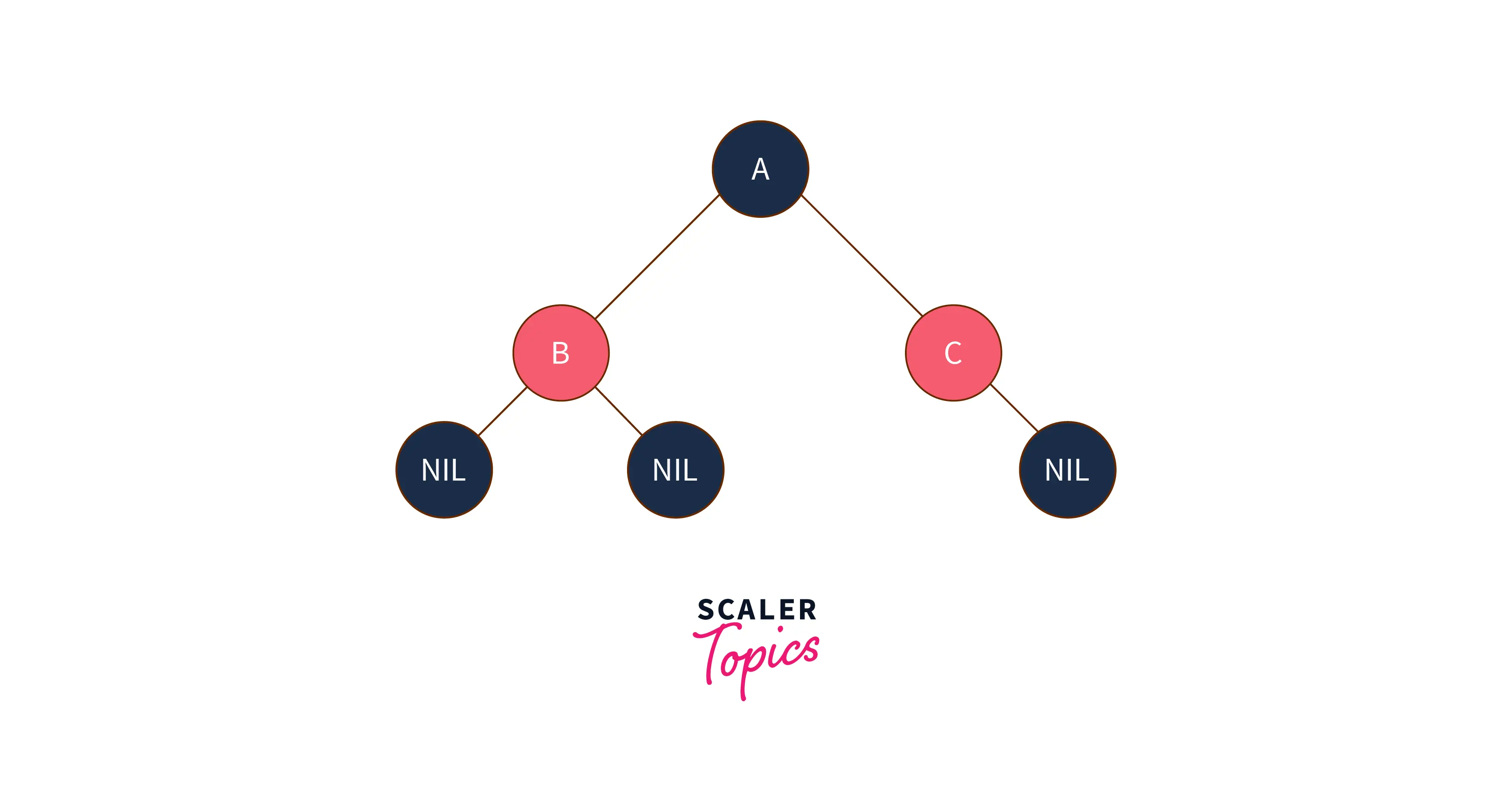
3. Red-Black Tree

The red-black tree is also a self-balancing tree. Each node is either painted red or black. The rules of a red-black tree are:

• The leaf nodes and root nodes are black.
• If a parent node is red, both children nodes are black.
• There cannot be two adjacent red nodes.
• Every path from a node to the descendant NULL node (end of the path) must have an equal number of black nodes.

To learn about the red-black tree in detail, refer to this.

4. B-Tree

A B-Tree is a self-balancing search tree that is specifically designed for disk storage systems. Here are the key properties of a B-Tree:

1. Uniform Leaf Level: All leaves of a B-Tree are guaranteed to be at the same level, ensuring efficient retrieval operations regardless of the tree’s size.
2. Minimum Degree ‘t’: The structure of a B-Tree is determined by its minimum degree ‘t’, which is influenced by the disk block size.
3. Key Constraints: Each non-root node must contain at least ‘t-1’ keys, while the root may have a minimum of one key. Additionally, all nodes, including the root, can hold at most ‘(2*t – 1)’ keys.
4. Child-Node Relationship: The number of children of a node is equal to the number of keys it contains plus one.
5. Sorted Keys: Keys within a node are always sorted in increasing order, facilitating efficient searching operations.
6. Leaf Node Insertion: New key insertion in a B-Tree occurs exclusively at leaf nodes, maintaining the balanced structure of the tree.

5. B+ Tree

A B+ tree is an enhancement of the B-tree data structure, specifically optimized for indexing purposes. Unlike traditional B-trees, which store data pointers in both internal and leaf nodes, B+ trees only store data pointers at the leaf nodes. This design eliminates the need to traverse internal nodes for data retrieval, making B+ trees more efficient for disk-based storage systems.

Key characteristics of a B+ tree include:

1. Leaf Node Structure: Leaf nodes in a B+ tree store all key values along with their corresponding data pointers to disk blocks.
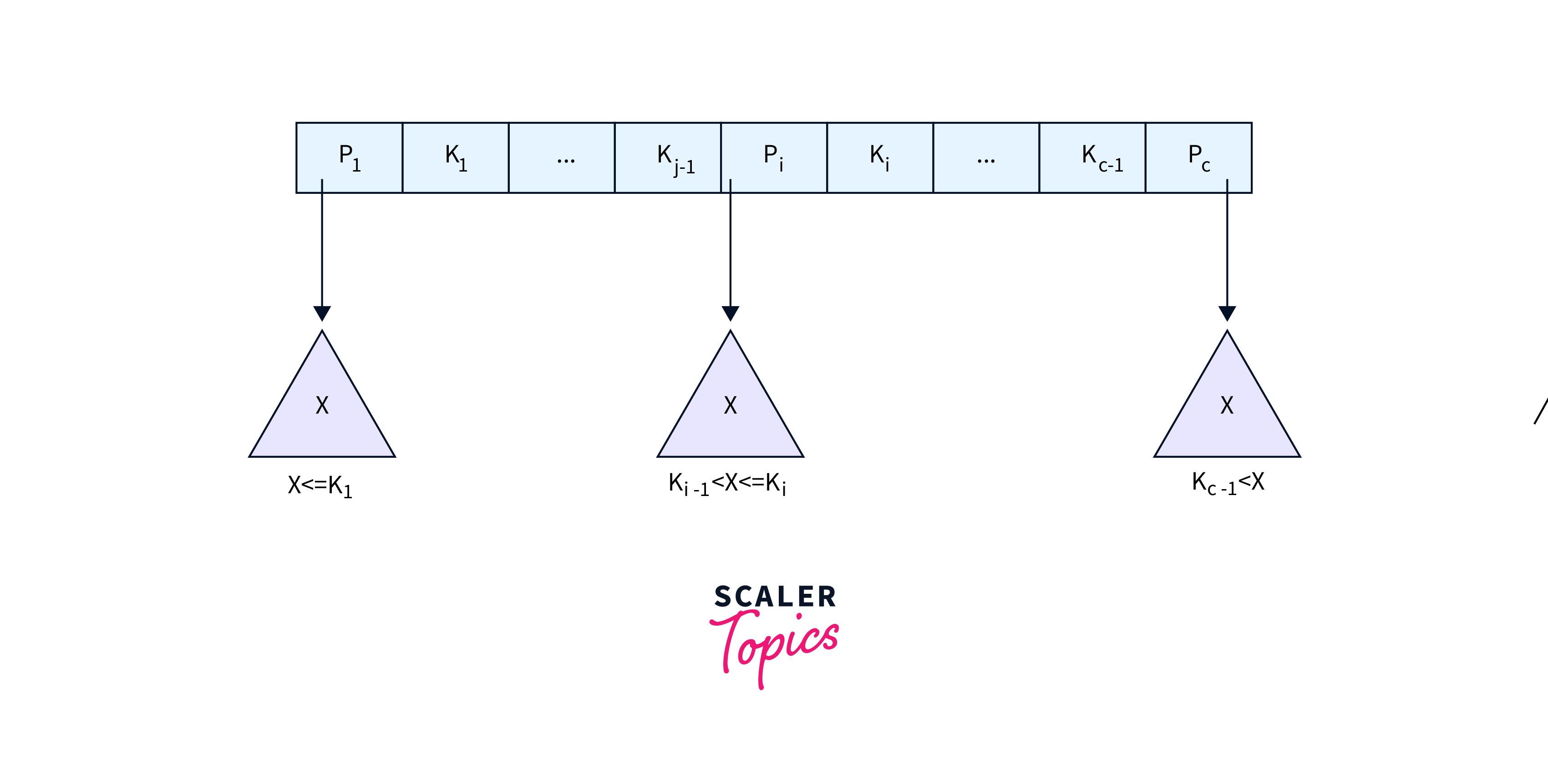
2. Internal Node Structure: Internal nodes of a B+ tree consist of tree pointers and key values. Each internal node follows a specific structure where keys are sorted in ascending order, facilitating efficient search operations.
3. Tree Pointer Arrangement: Internal nodes have a maximum of ‘a’ tree pointers, where ‘a’ is the order of the B+ tree. The root node contains at least two tree pointers, while other internal nodes have at least ⌈a/2⌉ pointers.
4. Key-Pointer Relationship: For each search field value ‘X’ in the subtree pointed to by a tree pointer Pi, the internal node ensures that the condition Ki-1 < X <= Ki holds for 1 < i < c, where ‘c’ is the number of pointers in the node.

6. Segment Tree

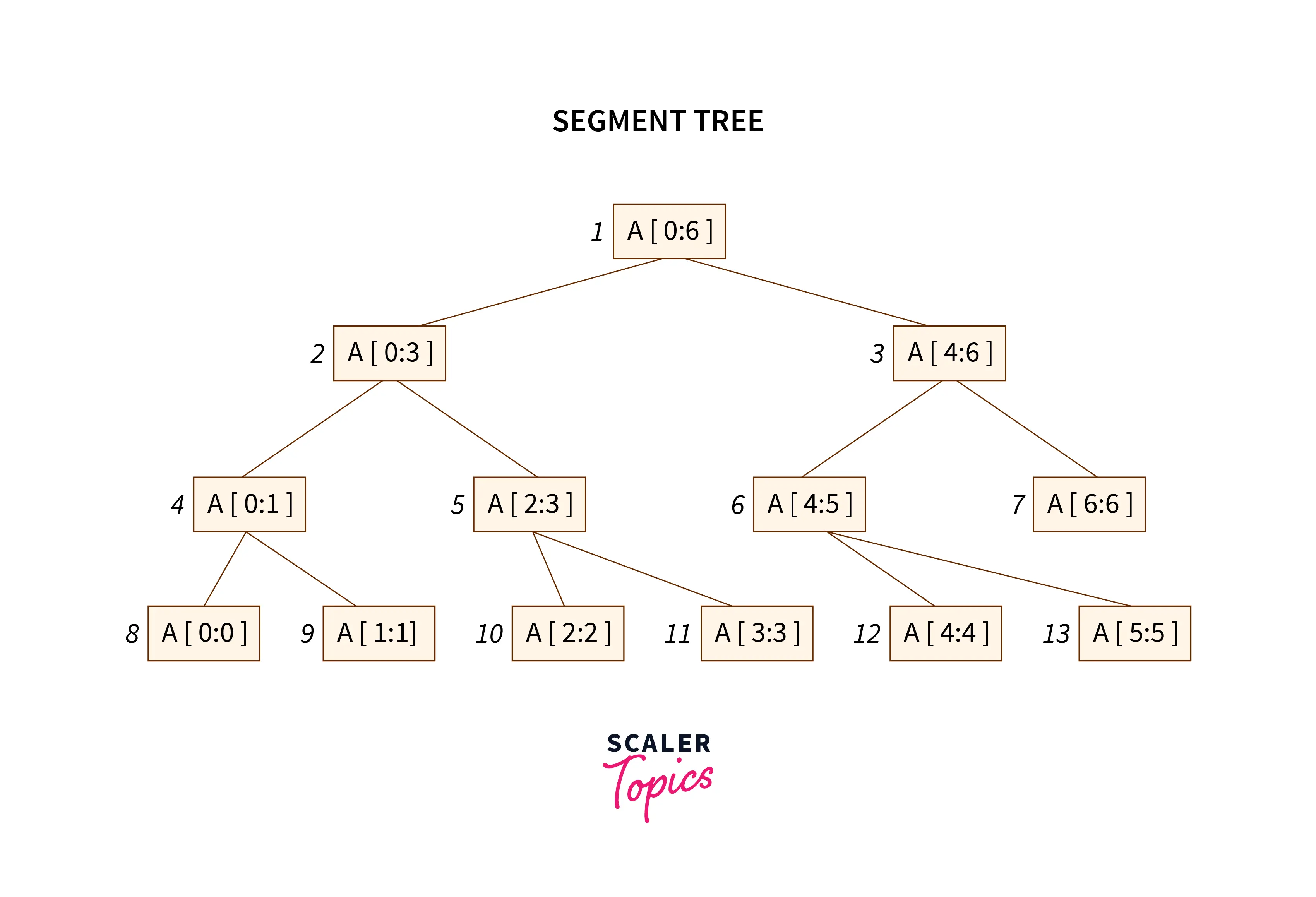
A segment tree is a binary tree utilized for storing intervals or segments. Every node of the tree is used to represent an interval. A segment tree can be represented using a simple array. This tree allows us to answer range queries over an array.

Let’s say we have an array A of size N that represents a segment tree T.

• The root node of the tree includes all elements of the array A[0 – 1].
• Every leaf node of the tree will represent only one element of the array A[i] such that 0 <= i < N
• The internal nodes of the tree will represent the union of elementary intervals A[i : j] where 0 <= i < j < N.

Two operations can be done on a segment tree – update (update the value of a key) and query (given two indices, return the segment lying between the two indices).

Conclusion

1. Trees are hierarchical data structures consisting of nodes, each storing a value and references to child nodes.
2. Binary trees restrict nodes to have at most two children, leading to variations like full, degenerate, perfect, complete, and balanced binary trees.
3. Ternary trees extend this concept, allowing nodes to have up to three children, typically labeled as “left”, “mid”, and “right”.
4. N-ary trees, also known as generic trees, permit nodes to have multiple children, with the exact number varying per node.
5. Binary Search Trees, AVL Trees, and Red-Black Trees are variants optimized for efficient searching, insertion, and deletion operations.
6. B-Trees and B+ Trees are designed for disk storage systems, ensuring uniform leaf levels and efficient indexing for large datasets. Additionally, segment trees offer a specialized structure for interval-based queries in arrays.