Wave Array

Problem Statement

Sort an unsorted array arr of length n in a waveform. An array is said to be in wave form if it satisfies the following conditions:

• The array elements in the output should be such that arr[0] >= arr[1] <= arr[2] >= arr[3] <= arr[4] …..
• If there are multiple sorted orders in wave form, print any one of the viable solutions.
• The unsorted array may contain duplicate values. (The array [7, 7, 11, 3, 4, 5, 15] can output wave arrays [4, 3, 7, 5, 11, 7, 15] or [ 7, 7, 11, 3, 5, 4, 15] or any other valid wave array. )

Example

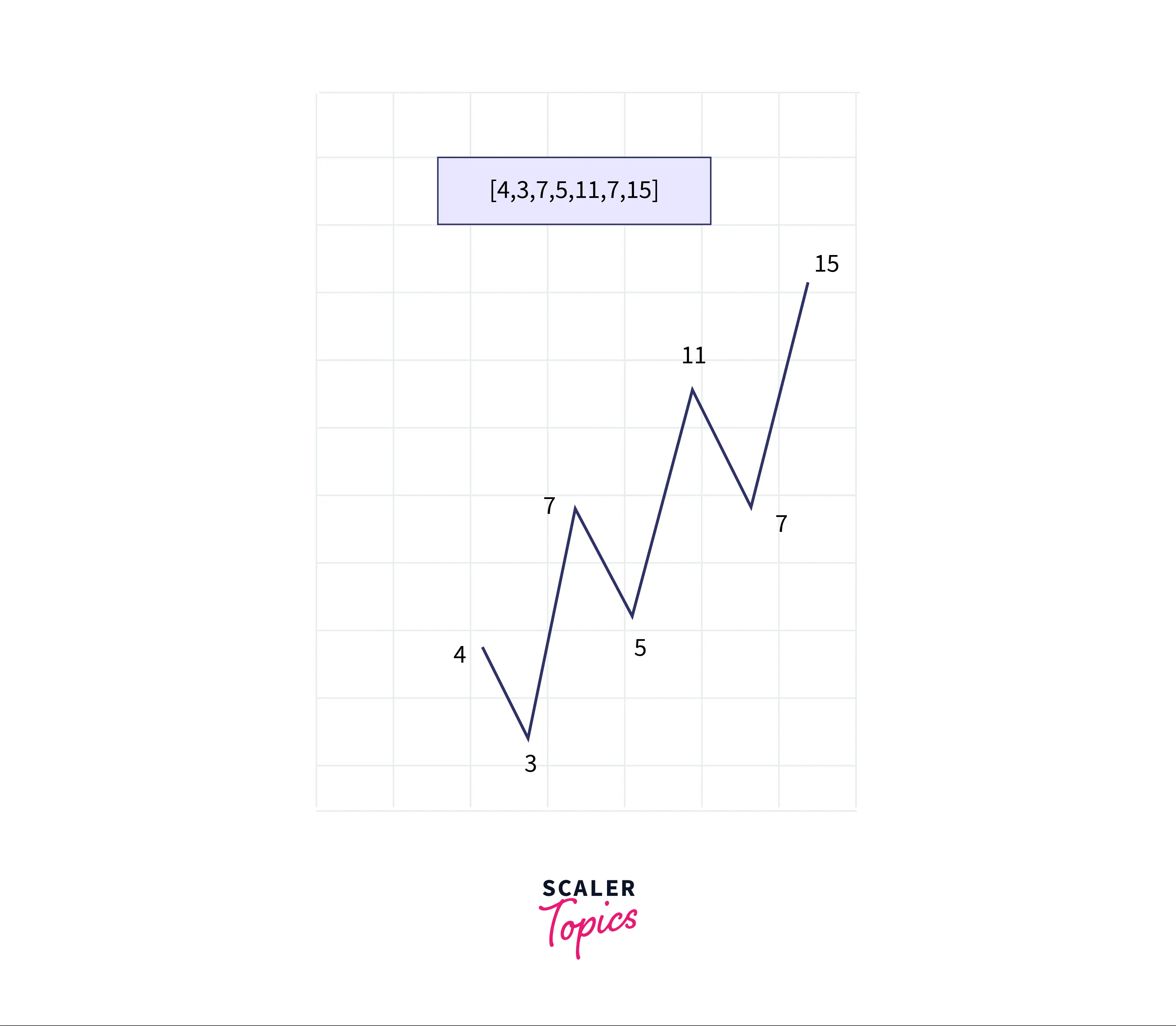
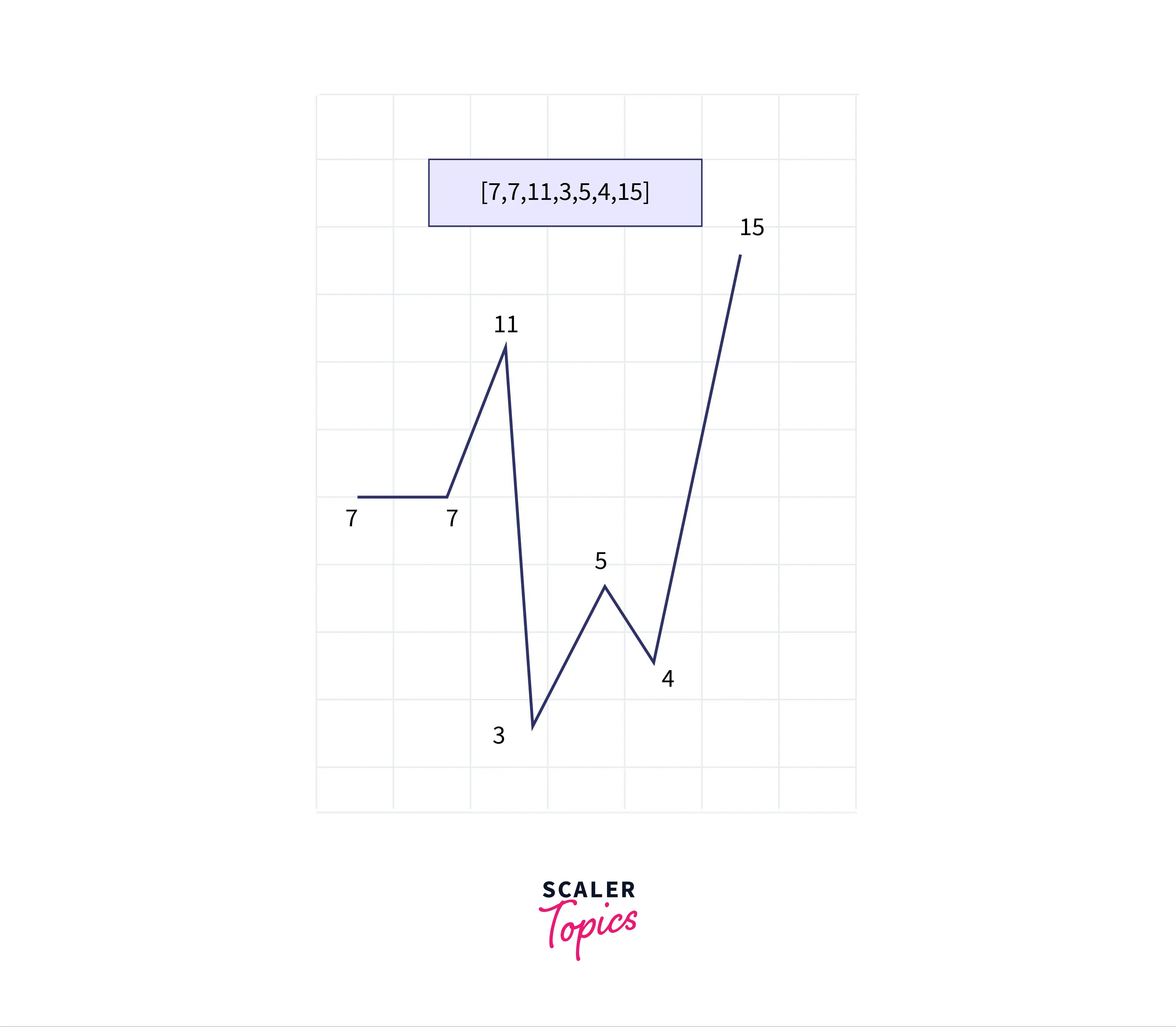
Example Explanation

Input: arr = [7, 7, 11, 3, 4, 5, 15] Output: [4, 3, 7, 5, 11, 7, 15] or any other array in wave form.

Explanation: In the above example, it can be seen that 4 >= 3 <= 7 >= 5 <= 11 >= 7 <= 15. Thus the resultant array will be [4, 3, 7, 5, 11, 7, 15] as it is sorted in wave form.

Input/Output

Input

• The first line of input contains integer n, which is the size of the array.
• The second line contains n space-separated elements of the unsorted array.

Output

• The output contains the array sorted in wave format.

Constraints

$1 ≤ n ≤ 10^{6}$

$0 ≤ arr[i] ≤ 10^{7}$

Algorithm 1 – Simple Brute Force Approach – Use Sorting and Swapping

Algorithm

• Step 1 – At the initial step, sort the input array in ascending order, (i.e. arr[0] <= arr[1] <= arr[2]…) 
  

• Step 2 – Next, on swapping the alternate elements (i.e. arr[0] with arr[1] and arr[2] with arr[3]..) a wave array is obtained. 

Note: This approach prints the lexicographically smallest array.

Code Implementation

C++

#include<iostream>
#include<algorithm>
using namespace std;
/* Function to swap two numbers.*/
void swap(int *x, int *y){
    int temp = *x;
    *x = *y;
    *y = temp;
}
/* Function to sort array in wave form, i.e., arr[0] >= arr[1] <= arr[2].....*/
int* waveArray(int arr[], int n){
    // Sorting
    sort(arr, arr+n);
    // Swapping
    for (int i=0; i<n-1; i += 2)
        swap(&arr[i], &arr[i+1]);
    return arr;
}
/*Driver code*/ 
int main(){
    int size = 7;
    int arr[7] = {7, 7, 11, 3, 4, 5, 15};
    
    cout<<"Input array elements: ";
    for(int i=0;i<size;i++){
        cout << arr[i] << " ";
    } cout << endl;
    
    waveArray(arr, size);
    int i;
    cout<<"The wave array will be: [";
    for(i=0;i<size-1;i++){
        cout<<arr[i]<<", ";
    }
    cout<<arr[i]<<"]";
    return 0;
}

Java

import java.io.*;
import java.util.*;  
class Main
{
    /* Function to swap two numbers.*/
    void swap(int arr[], int x, int y){
        int temp = arr[x];
        arr[x] = arr[y];
        arr[y] = temp;
    }
 
    //* Function to sort array in wave form, i.e., arr[0] >= arr[1] <= arr[2].....*/
    void waveArray(int arr[], int n){
        // Sorting
        Arrays.sort(arr);
        // Swapping
        for (int i=0; i<n-1; i += 2)
            swap(arr, i, i+1);
    }
 
    /*Driver code*/ 
    public static void main(String args[]){
        int size = 7;  
		int[] arr = {7, 7, 11, 3, 4, 5, 15};  
		System.out.print("Input array elements: ");  
		for(int i=0; i<size; i++){
		    System.out.print(arr[i] + " ");
		}  
		System.out.println();
        Main wave = new Main();
        wave.waveArray(arr, size);
        System.out.print("The wave array will be: ["); 
        int i;
        for(i=0; i<size-1; i++)
            System.out.print(arr[i] + ", ");
        System.out.println(arr[i] + "]");
    }
}

Python

"""Function to sort array in wave form, i.e., arr[0] >= arr[1] <= arr[2]....."""
def waveArray(arr, n):
    """
    :type arr: List[int]
    :type n: int
    :rtype: arr
    """
    # Sorting
    arr.sort()
    #Swapping
    for i in range(0,n-1,2):
        arr[i], arr[i+1] =  arr[i+1], arr[i]
    return arr
#Driver Code
if __name__ == '__main__':
	size= 7
	arr = [7, 7, 11, 3, 4, 5, 15]
	print("Input array elements: ", *arr)
	print("The wave array will be:", end=" ")
	print(waveArray(arr, size))

Output

Input array elements: 7 7 11 3 4 5 15 
The wave array will be: [4, 3, 7, 5, 11, 7, 15]

Time complexity

On using heap sort, the time complexity for sorting becomes O(n * logn). To swap elements the entire array needs to be traversed. Hence the time complexity for swapping is O(n). Therefore, the total time complexity for this approach will be O(n * logn).

Space complexity

Since heap sort is being used no additional space is required. Thus, the space complexity for this approach will be O(1).

Algorithm 2 – Comparing Neighbors

Algorithm

• Step 1 – At the initial step, traverse all even positioned elements of the input array such that
  • If the current element is smaller than the previous element (positioned at the odd index), swap the elements at the previous and current index.
  • If the current element is smaller than the next element (positioned at the odd index), swap the elements at the next and current index.

Code Implementation

C++

#include<iostream>
#include<algorithm>
using namespace std;
/* Function to sort array in wave form, i.e., arr[0] >= arr[1] <= arr[2].....*/
void waveArray(int arr[], int n){
    /* Traversing all even positioned elements*/
    int i = 0;
    while (i < n) { 
        /* If the current even index element is smaller than the previous */
        if (i > 0 && arr[i-1] > arr[i] ) 
            swap(arr[i], arr[i-1]);
        /* If the current even index element is smaller than the next */
        if (i < n-1 && arr[i] < arr[i+1] ) 
            swap(arr[i], arr[i + 1]);
        i = i + 2;
    } 
}
/*Driver code*/ 
int main(){
    int size = 7;
    int arr[7] = {7, 7, 11, 3, 4, 5, 15};
    cout<<"Enter array elements: ";
    for(int i=0;i<size;i++){
        cout << arr[i] << " ";
    }cout << endl;
    waveArray(arr, size);
    cout<<"The wave array will be: [";
    int i;
    for(i=0;i<size-1;i++){
        cout<<arr[i]<<", ";
    }
    cout<<arr[i]<<"]";
    return 0;
}

Java

import java.io.*;
import java.util.*;  
class Main{
    /* Function to swap two numbers.*/
    void swap(int arr[], int x, int y){
        int temp = arr[x];
        arr[x] = arr[y];
        arr[y] = temp;
    }
 
    /* Function to sort array in wave form, i.e., arr[0] >= arr[1] <= arr[2].....*/
    void waveArray(int arr[], int n){
        /* Traversing all even positioned elements*/
        int i = 0;
        while (i < n) { 
            /* If the current even index element is smaller than the previous */
            if (i > 0 && arr[i-1] > arr[i] ) 
                swap(arr, arr[i], arr[i-1]);
            /* If the current even index element is smaller than the next */
            if (i < n-1 && arr[i] < arr[i+1] ) 
                swap(arr, arr[i], arr[i + 1]);
            i = i + 2;
        } 
    }
    /*Driver code*/ 
    public static void main(String args[]){
        int size = 7;  
		int[] arr = {7, 7, 11, 3, 4, 5, 15};  
		System.out.print("Input array elements: ");  
		for(int i=0; i<size; i++){
		    System.out.print(arr[i] + " ");
		}  
		System.out.println();
        Main wave = new Main();
        wave.waveArray(arr, size);
        System.out.print("The wave array will be: ["); 
        int i;
        for(i=0; i<size-1; i++)
            System.out.print(arr[i] + ", ");
        System.out.println(arr[i] + "]");
    }
}

Python

"""Function to sort array in wave form, i.e., arr[0] >= arr[1] <= arr[2]....."""
def waveArray(arr, n):
    """
    :type arr: List[int]
    :type n: int
    :rtype: arr
    """
    #Traversing all even positioned elements
    for i in range(0,n-1,2):
        # If the current even index element is smaller than previous 
        if (i > 0 and arr[i-1] > arr[i] ):
            arr[i], arr[i-1] = arr[i-1], arr[i]
        # If the current even index element is smaller than next 
        if (i < n-1 and arr[i] < arr[i+1] ):
            arr[i], arr[i+1] = arr[i+1], arr[i]
    return arr
#Driver Code
if __name__ == '__main__':
	size= 7
	arr = [7, 7, 11, 3, 4, 5, 15]
	print("Input array elements: ", *arr)
	print("The wave array will be:", end=" ")
	print(waveArray(arr, size))

Output

Input array elements: 7 7 11 3 4 5 15 
The wave array will be: [7, 7, 11, 3, 5, 4, 15]

Time Complexity

Since the entire array needs to be linearly traversed the time complexity for this approach will be O(n).

Space Complexity

Since no extra space is required the space complexity for this approach will be O(1).

Conclusion

• A wave array is an array that follows a particular sequence such that arr[1] >= arr[2] <= arr[3] >= arr[4] <= arr[5]….
• Approach 1 – The input array is sorted, and all the adjacent elements are swapped.
  • Time Complexity – O(n logn)
  • Space Complexity – O(1)
• Approach 2 – The input array is rearranged such that all even positioned (at index 0, 2, 4, ..) elements are greater than their adjacent odd elements.
  • Time Complexity – O(n)
  • Space Complexity – O(1)

FAQ

Q. Which of the above approaches prints the lexicographically smallest array?

A.The first approach includes sorting(in ascending order) that results in the output being the lexicographically smallest array.

Q. State whether the following statement is True or False. If the input array is already sorted, then the output according to the second approach will be a lexicographically smallest array.

A. True. Since the array is already sorted, swapping adjacent elements will output the lexicographically smallest array.