What is Hamming code?

When we are transmitting data from sender to receiver, there might be a chance of error in the data while transmitting, Hamming code is the set of codes that helps in error detection as well as error correction in the data during transmission. The prerequisite for understanding the basics of error detection and correction can be studied from here.

The error can be due to interference and network problems and many external factors.

Introduction to Hamming Code

Hamming Code is the set of error-correction codes that are used to detect the error in the transmitted data and to correct the error. It can be applied to data units of any length.

Hamming code is generally used for detecting as well as correcting single-bit errors.
Generally, the source encodes the message by adding a few redundant bits during the transmission.

These redundant bits are generated and inserted at certain positions in the message. They are mostly used for error detection and correction process.

Redundant Bits

So let’s get into detail about the implementation of Hamming Code. Implementation of Hamming code uses redundant bits. Firstly what is a redundant bit?
Redundant bits are the extra bits that are added by the sender and removed(decoded) by the receiver.

They are generated by following the below algorithm. These extra redundant bit help not only in error detection but also in error correction by indicating at which bit the error occurred.

The number of redundant bits required can be calculated using the below formula below:

$$ 2^R ≥ M + R + 1 $$

where, R = Number of redundant bits,

M = Number of data bits

Determining the Position of Redundant Bits

For instance, if data bits are 4 then the number of redundant bits can be calculated as
$$ 2^3 >= 4+3+1 $$
where 3 is the required number of redundant data bits so that no data is lost during the transmission.

Parity Bits

Parity bits are nothing but redundant bits that are added to oversee that no data is being lost during transmission. These extra bits are basically used for error detection at the receiver point.
There are two types of parity bits, which are:

Odd Parity bit:

• To find the value of a parity bit we need to check the number of ones in the data.
• So, the number of ones is counted, if the count is even then the odd parity bit’s value is set to 1 and vice-versa if the count is odd, i.e parity bit’s value is set to 0.

Even parity bit:

• In the same way as in the Odd parity bit, we first need to count the number of ones present in the given data. And then accordingly we need to assign the value.
• If the count is even then even parity bit’s value is assigned as 0.
• If the count is odd then the even parity bit’s value is assigned as 1.

Determining the Parity Bits

Now, let’s discuss about the position of parity bits:

Parity bits are placed at the bit position which is the power of 2 i.e, ( 2^0^ , 2^1^, 2^2^, 2^3^, 2^4^ ,…. so on) which are (1,2,4,8,... so on). So for example, in the 7-bit data transfer we will be having 4 parity bits which are (1,2,4,8).

General Algorithm of Hamming Code

The Hamming Code is calculated in the following way. This is simply the use of extra redundant/parity bits for the detection and correction of an error that occurred while transmitting the data.

1. Firstly, write all the bit positions which are starting from 1 in the binary form i.e (1, 10, 11, 100, etc.).
2. All the bit positions that are a power of 2 are marked as parity bits (1, 2, 4, 8, etc).
3. All the other bit positions are treated as data bits and we need to insert the given data in these bits which are required to find the value of parity bits.
4. Value of each parity bit, is determined in the following way(The position of the parity mainly determines the sequence of bits that it alternatively checks and skips.).
   • Parity bit 1 at position R1: Check 1 bit, then skip 1 bit, check 1 bit and then skip 1 bit and so on, like:
     Example: 1, 3, 5, 7, 11, etc.Parity bit 2 at position R2: Check 2 bits, then skip 2 bits, check 2 bits, then skip 2 bits, like:
     Example: 2, 3, 6, 7, 10, 11, 14, 15, etc.Parity bit 3 at position R4: Check 4 bits, then skip 4 bits, check 4 bits, then skip 4 bits, like:
     Example: 4, 5, 6, 7, 12, 13, 14, 15, etc.Parity bit 4 at position R8: Check 8 bits, then skip 8 bits, check 8 bits, then skip 8 bits, like:
     Example: 8, 9, 10, 11, 12, 13, 14, 15, 24, 25, 26, 27, 28, 29, 30, 31).This can be clearly explained using the below image

5. We usually check for even parity, So if the count of the number of ones from respective bits is even assign the value of the respective redundant bit as 0 and vice-versa.

Example of Hamming Code

For an example of 4 data bits, we need to determine the number of redundant bits required and the position of each redundant bits:
We know that the redundancy bits are placed at positions that are a power of 2 i.e, 1,2,4,8,16,..so on.
Let’s consider an example:

Number of data bits to be transmitted = 4
Number of redundant bits required for
According the formula:

$$ 2^R ≥ M + R + 1 $$

where, R = Number of redundant bits,
M = Number of data bits

$$ 2^3 >= 4+3+1 $$

Therefore the number of redundant
bits for lossless of data during transmission is 3
Therefore the total number of bits obtained are(redundant bits + data bits)

$$ 3+4 =7 $$

The redundant bits are placed at positions corresponding
to the power of 2 i.e (1, 2, 4, 8, 16…etc)

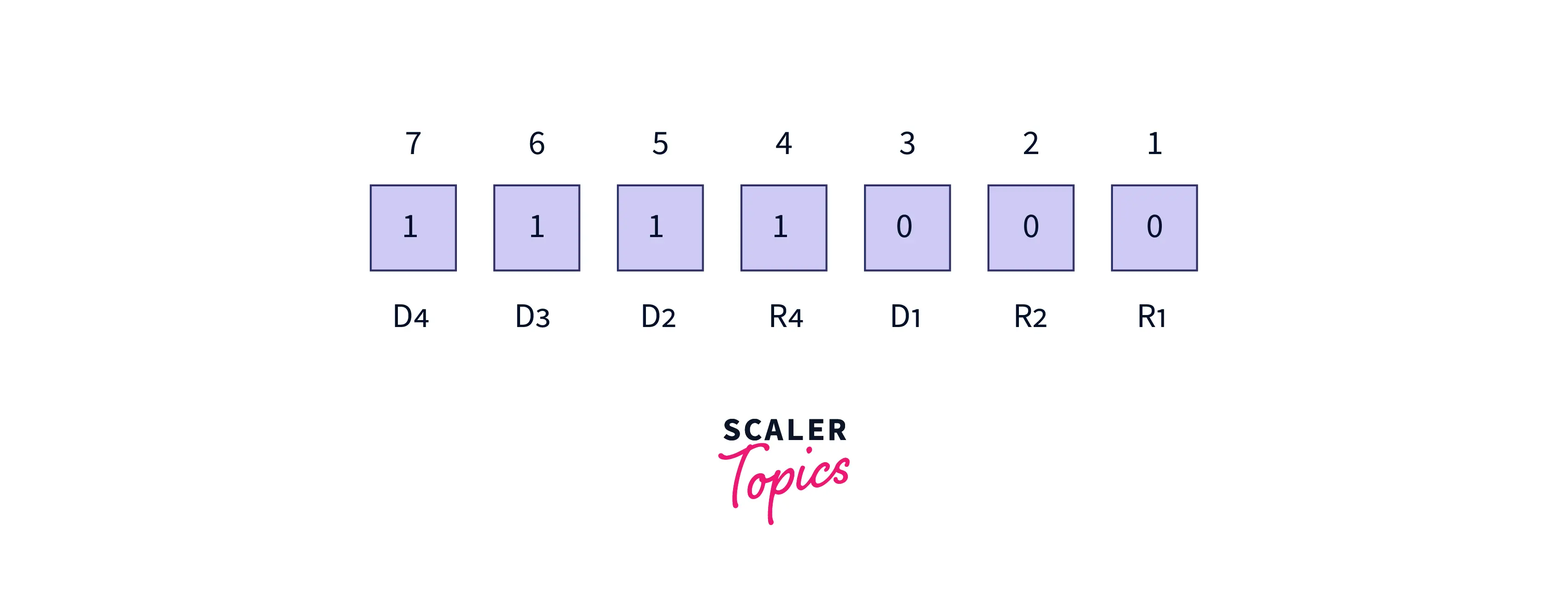
The below image explains it more clearly about it:

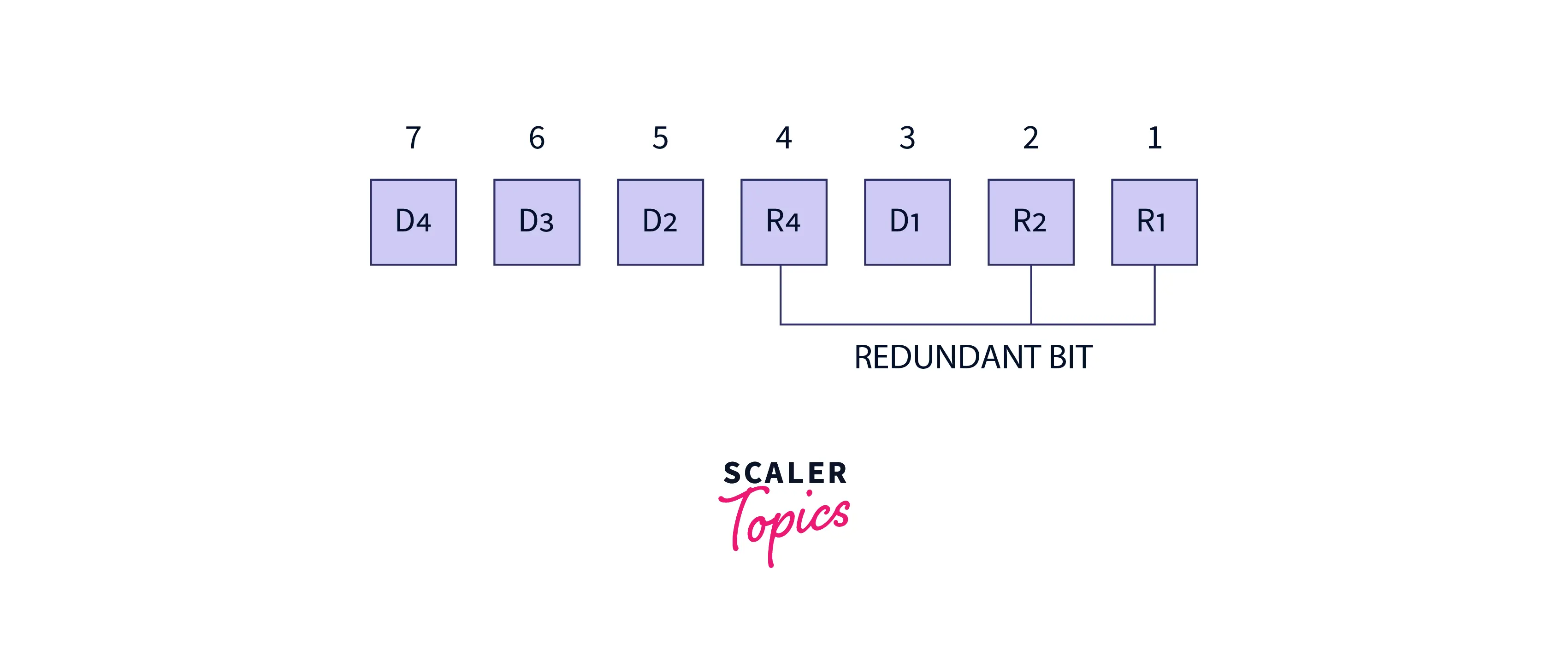
Where D represents data bit and R represents parity bit.
Let’s suppose the data to be transmitted is 1110 the bit will be placed as follows:

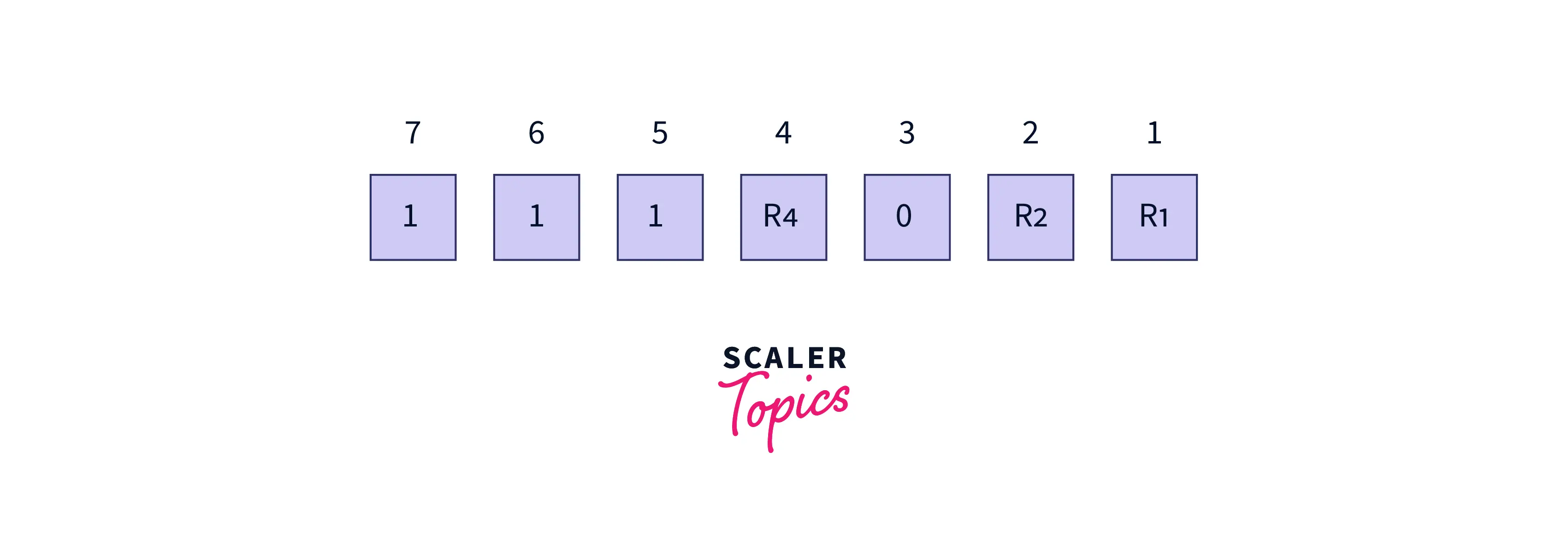
The third step includes determining the value of parity bits:

1. To find the value of R1: Follow this- check 1 bit, then skip 1 bit, check 1 bit and then skip 1 bit, and so on.
   R1 bits: 1, 3, 5, 7, 9, 11.. so on, Since the total number of bits is 7. So, R1 bits are: 1, 3, 5, 7.
   This is clearly explained using the image:

This image is just an example but the value in the bits should be like in the next image attached here(same for all below cases)

Mathematically:
R1 = even parity(1, 3, 5, 7) = 0
For the value of redundant bit R1, we check for even parity. Since the total number of 1’s in all the bit positions corresponding to R1 is an even number the value of R1 (parity bit’s value) = 0

2. To find the value of R2: Follow this- check 2 bits, then skip 2 bits, check 2 bits and then skip 2 bits, and so on.
   R2: bits 2, 3, 6, 7

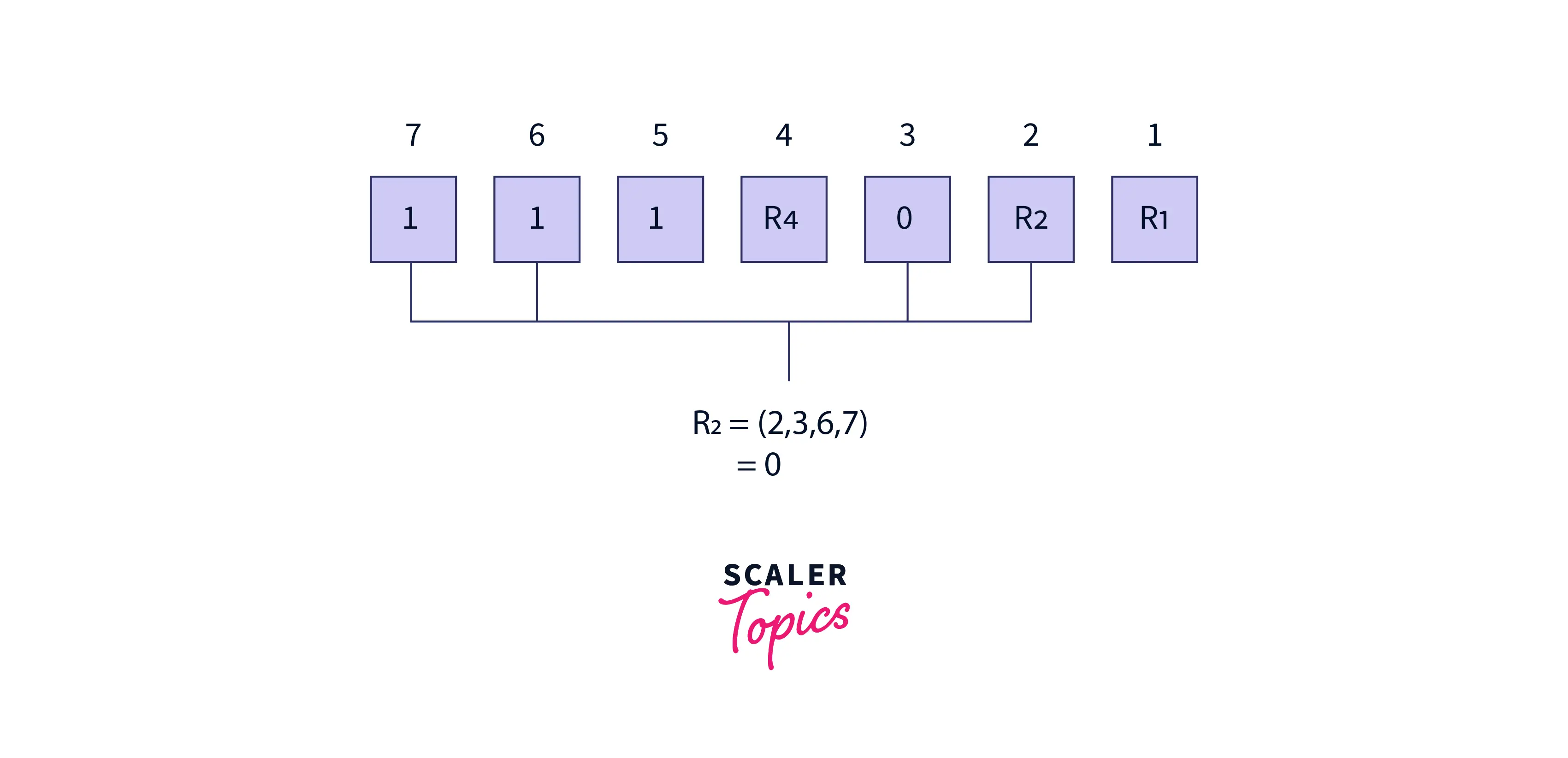
Mathematically:
R2 = even parity(2, 3, 6, 7) = 0
For the value of redundant bit R2, we check for even parity. Since the total number of 1’s in all the bit positions corresponding to R2 is an even number the value of R1 (parity bit’s value) = 0

3. To find the value of R4: Follow this check 4 bits, then skip 4 bits, check 4 bits and then skip 4 bits, and so on.
   R4: bits 4, 5, 6, 7

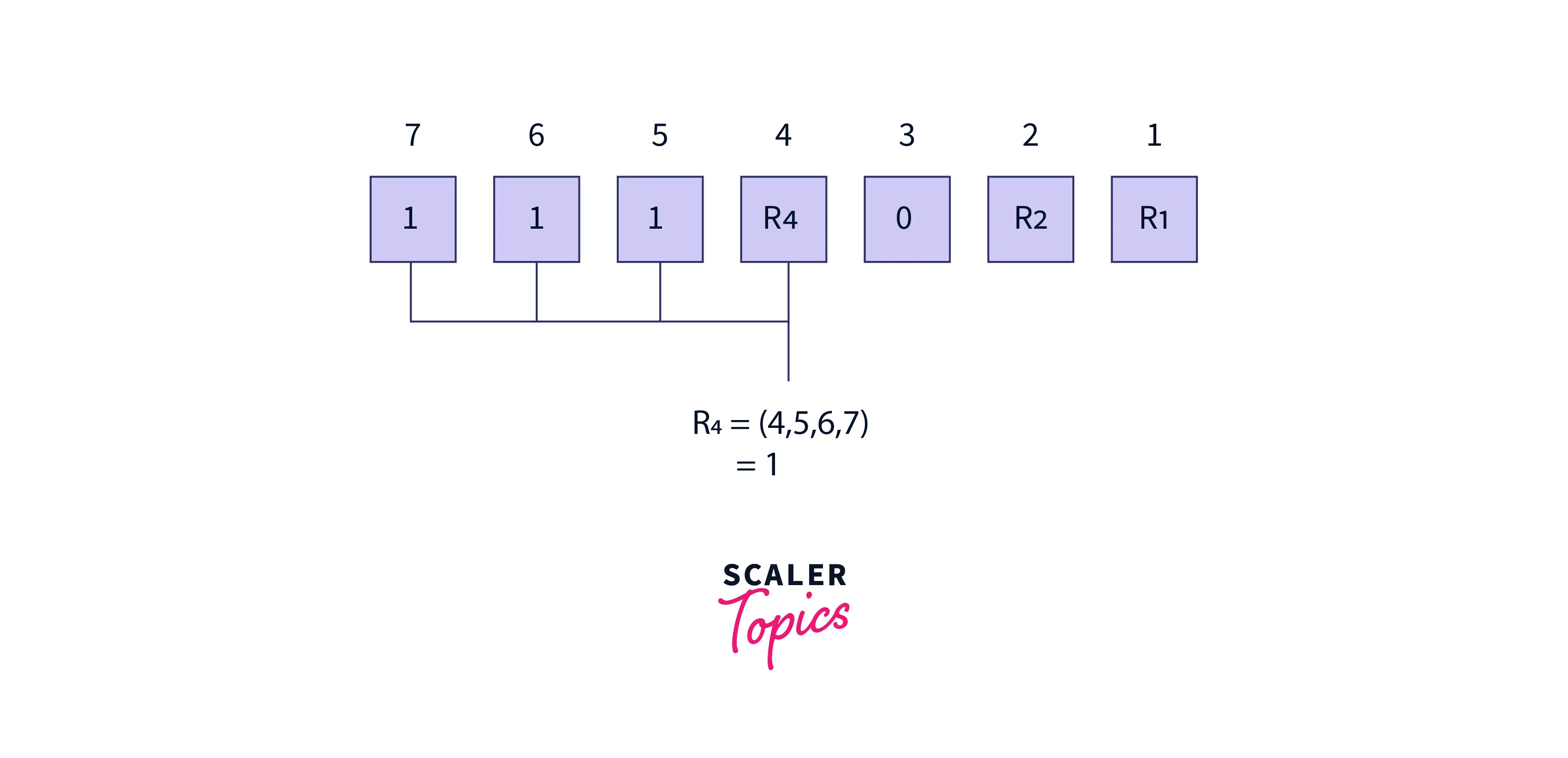
Mathematically:
R4 = even parity(4, 5, 6, 7) = 1
For the value of redundant bit R4, we check for even parity. Since the total number of 1’s in all the bit positions corresponding to R4 is odd number the value of R1 (parity bit’s value) = 1

Thus the data which will be transferred is:

Error Detection and Correction using Hamming Code

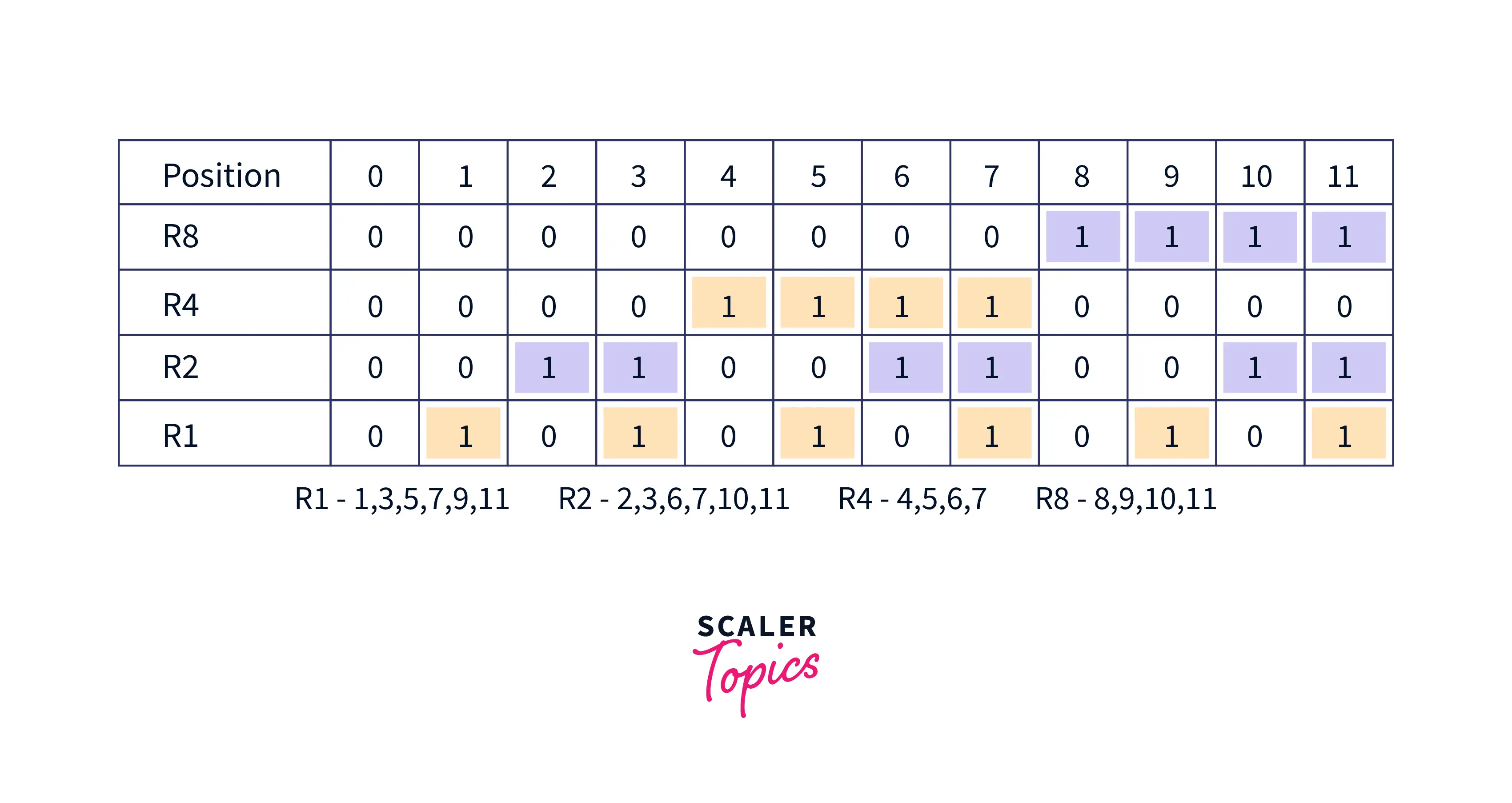
Suppose in the below example if the 10^th^ bit is changed from 0 to 1 during data transmission due to several external and internal factors, then it changes the parity values in the binary number which is formed:

• So to calculate the position of error we make use of values present in redundant bits/parity bits. These bits give the binary number representation as 1010 whose decimal value is 10.
• To calculate the binary representation as 1010, we need to do the parity check for positions of bits like we do for calculating the value of all redundant bits, i.e for R1, R2, R4, R8.
• And each bit in 1010 is values obtained by :
  • Bit 1(from right hand side): parity(1, 3, 5, 7, 9, 11) = 1 (observe from the image)
  • Bit 2(from right hand side): parity(2, 3, 6, 7, 10, 11) = 0
  • Bit 3(from right hand side): parity(4, 5, 6, 7) = 1
  • Bit 4(from right hand side): parity(8, 9, 10, 11) =0
  • Mathematically, 1010 is the binary representation of the error bit.
• Therefore, we can conclude that bit 10 contains an error. To correct the error the 10th bit is (toggled) i.e, changed from 0 to 1.

Advantages of Hamming Code

In this section, we will discuss the advantages of Hamming Code:

• Hamming codes are considered to be ideal for computer memory and single-error correction.
• Hamming code not only detects errors but also helps in the identification of bits on which error has occurred so that they can be corrected by the error detection procedure explained above.
• It is considered more efficient where the data streams are delivered for single-bit mistakes.

Disadvantages of Hamming Code

Despite having advantages Hamming Code also has a disadvantage:

• Hamming code is considered to be ideal for single-bit error correction but what if there are multiple bits where an error occurred? Hamming Code doesn’t come handy during this issue(not efficient).

Applications of Hamming Code

These are common applications which use Hamming Code:

• Computer Memory
• Open connectors
• Satellites
• Modems
• PlasmaCAM
• Embedded Processor

Conclusion

• Hamming code is a technique that was developed by R.W.Hamming to detect errors and correct them.
• Data can be transmitted during communication without any corruption.
• Hamming code is a set of liner code that is useful for error detection up to two immediate bit errors.
• It is also capable of single-bit errors.
• Few applications of using Hamming code are Modems, Satellites, Embedded Processor, Computer Memory, etc.
• With the use of Hamming Code, we can encrypt and decode the data while transmitting and after transmitting.
• The major advantage of Hamming Code is only during single bit errors, it fails when multiple bit errors occurred during communication in networks.
• To know more about parity bits in real-life application: Raid in DBMS