In a Binary Search Tree, the Inorder Successor of a given node is defined as the node with the smallest value greater than the value of the given node.
It can also be defined as the node next to the current node in the Inorder Traversal of the tree, as inorder traversal of BST returns the nodes in ascending order of their values. Inorder Successor for the last node is NULL.
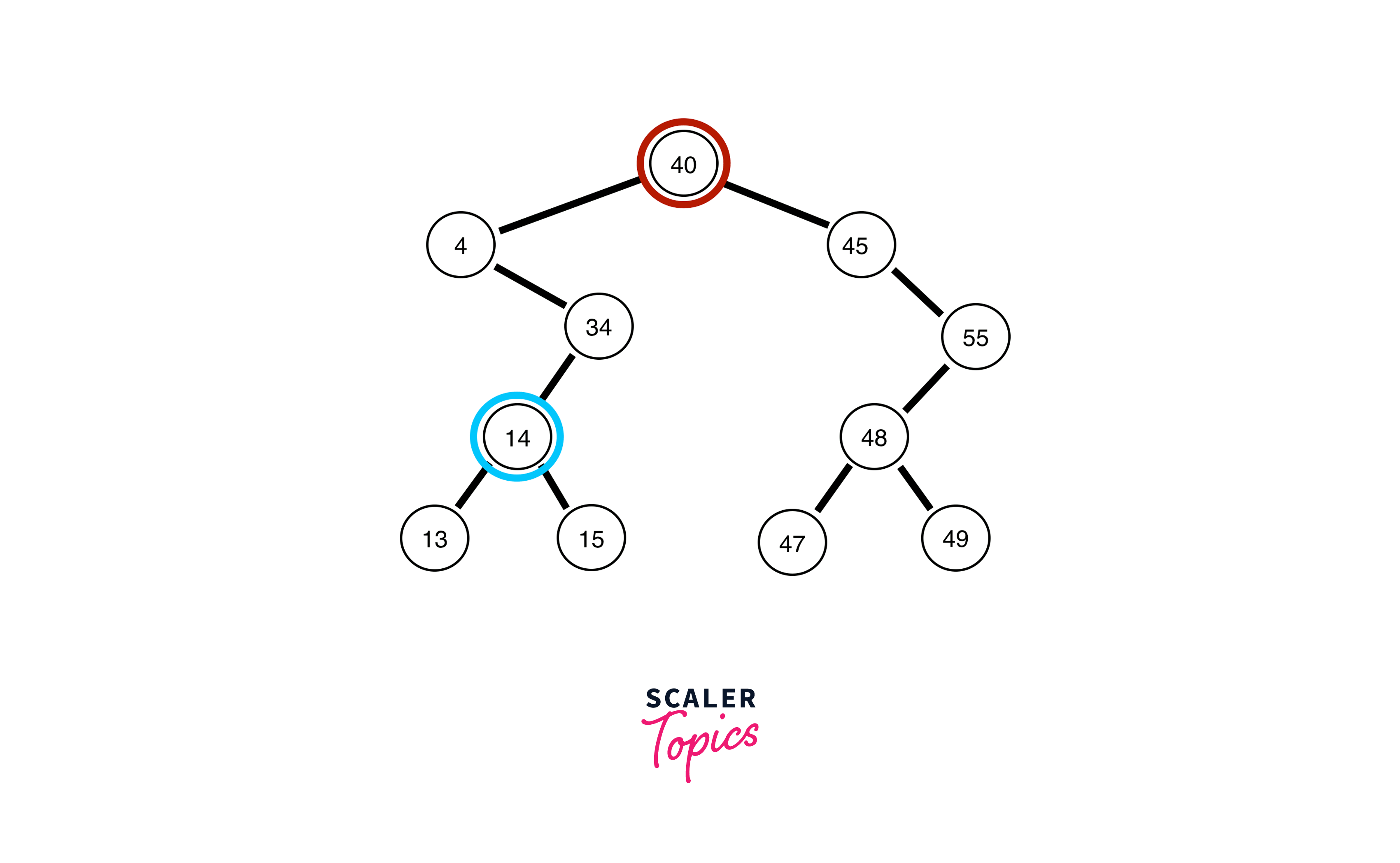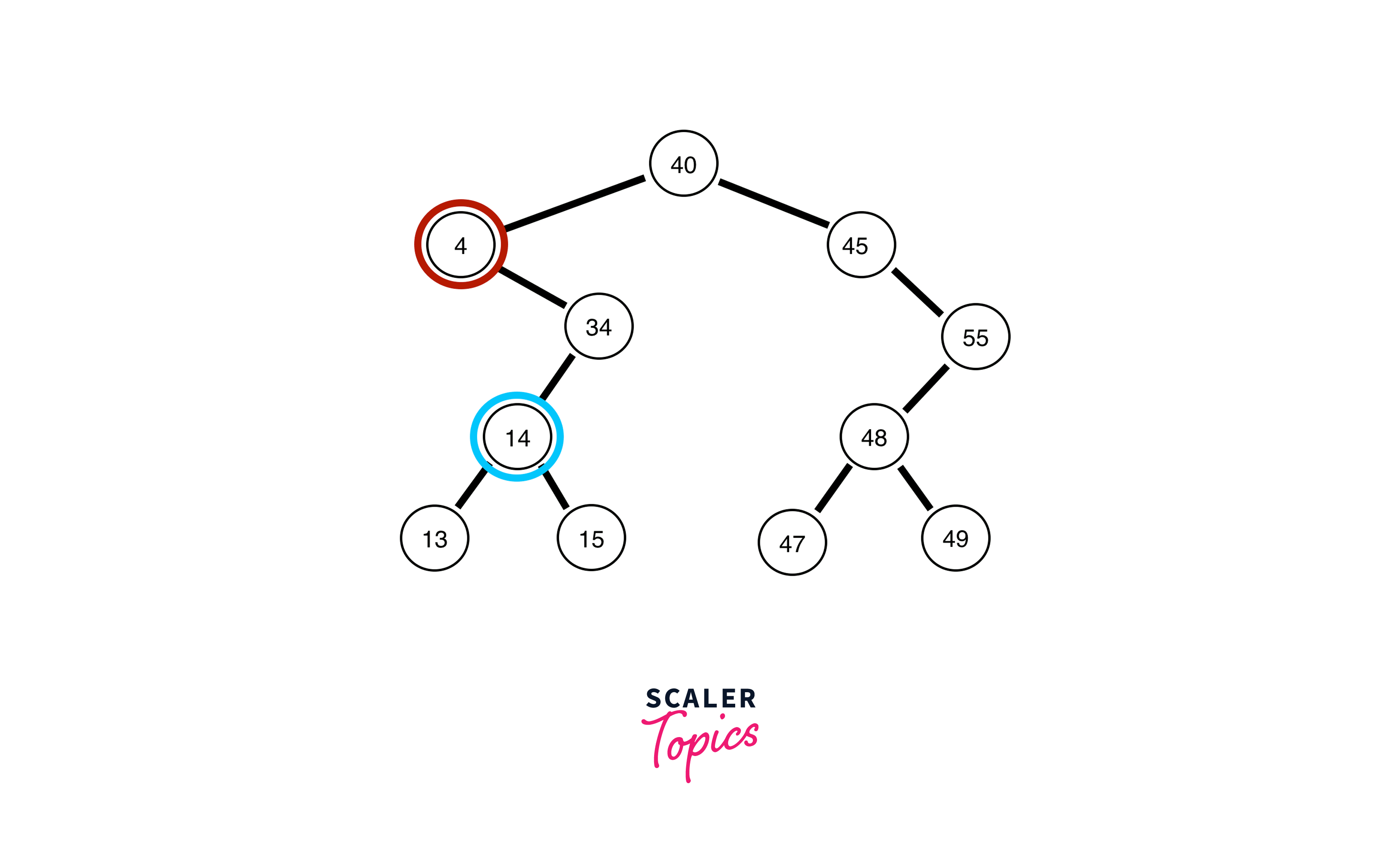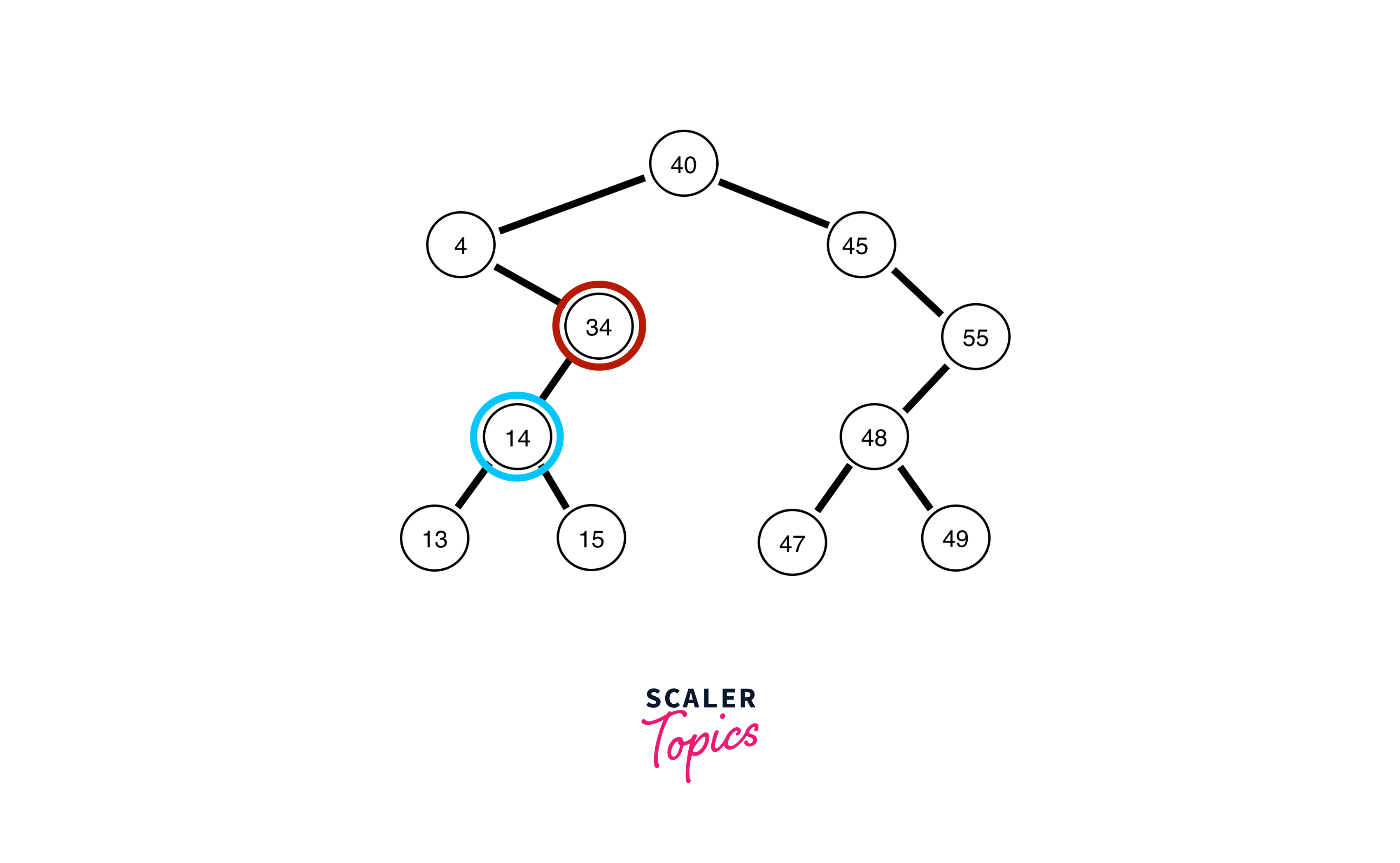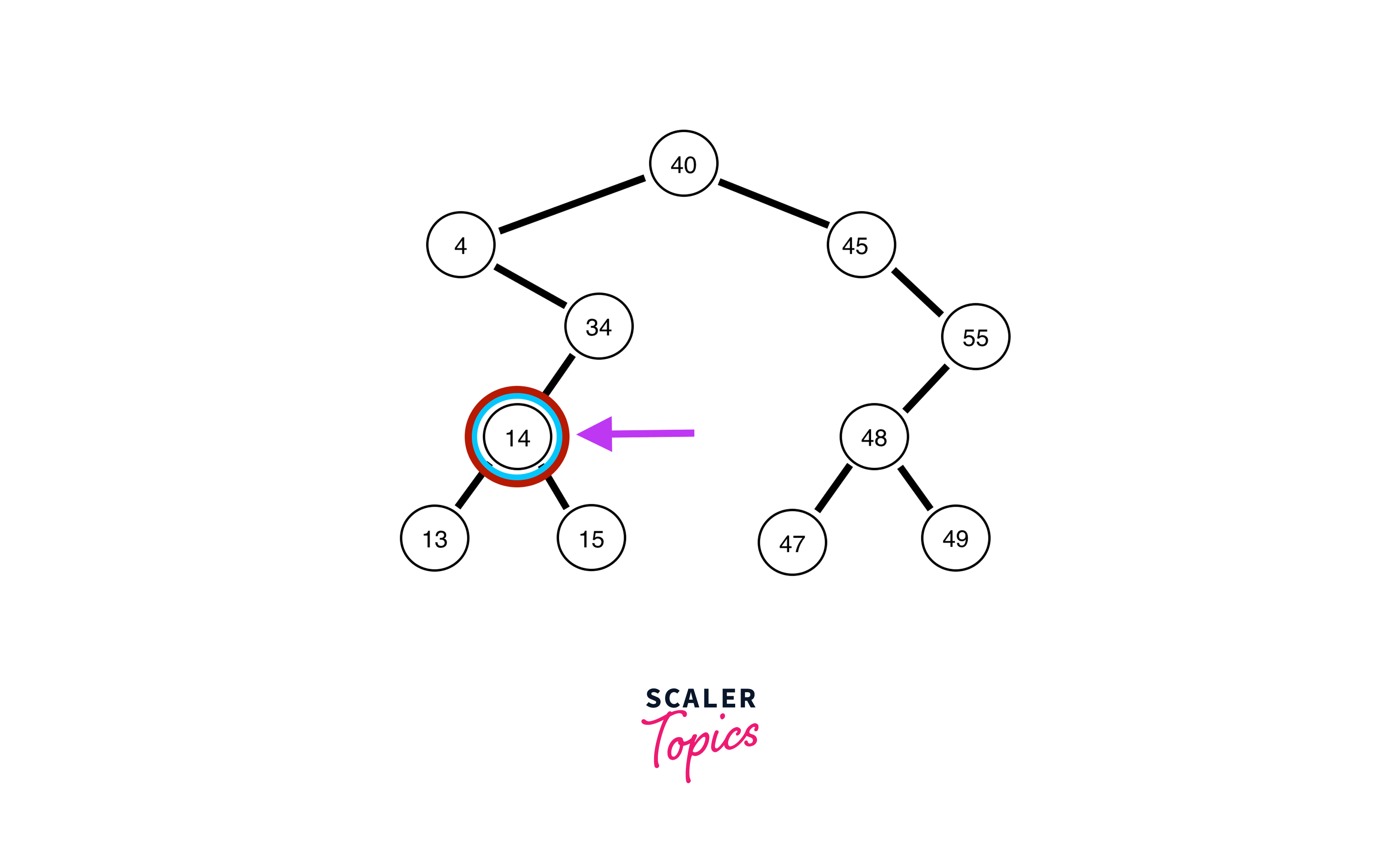
Example

In the above diagram, inorder successor of 8 is 10, inorder successor of 10 is 11 and inorder successor of 20 is 25.
Where to Find the Inorder Successor?
- If a node has a right child, its successor is the node with the least value present in its right sub-tree. The traversal proceeds towards the right sub-tree of the given node, and the minimum value is present in the leftmost descendant.
- If the given node does not have a right child, its in-order successor is located above it in the tree. While unfolding the recursive calls, the in-order traversal first visits the node whose left child was the most recent input. So, the successor of the given node is the parent of the node’s youngest ancestor which is a left child.
How to Find the Inorder Successor in Binary Search Tree?
Method 1 (Uses Parent Pointer)
Algorithm
- Step 1 – Assume that every node has a parent pointer.
- Step 2 – Check the right subtree of input node.
- If right subtree of node exists, then successor (succ) lies in right subtree. The node with minimum key value in the right subtree is returned.
- If the node does not contain a right subtree the successor (succ) is one of the ancestors. The parent pointer is used to travel up until a node is found which is the left child of its parent. The parent of such a node is the successor.
Code Implementation C++
#include <iostream>
using namespace std;
// Structure of a BST node
struct Node{
int val;
Node* left = nullptr;
Node*right = nullptr;
Node* parent = nullptr;
Node() {}
Node(int val): val(val) {}
};
// Recursive function to insert a key into a BST
Node* insert(Node* root, int key){
// create a new node if the root is null
if (root == nullptr)
return new Node(key);
Node* temp;
if (key < root->val){
temp = insert(root->left, key);
root->left = temp;
temp->parent = root;
}
else{
temp = insert(root->right, key);
root->right = temp;
temp->parent = root;
}
return root;
}
// Function to find minimum value node in a given BST
Node* findMinimum(Node* root){
while (root->left)
root = root->left;
return root;
}
// function to locate node whose inorder successor is to be found
Node * SearchBST(Node * root, int key) {
if (root == NULL or root->val == key)
return root;
else if (root->val < key)
return SearchBST(root->right, key);
else if (root->val > key)
return SearchBST(root->left, key);
return NULL;
}
/* Function to find an inorder successor */
Node* InorderSuccessor(Node* root, int node){
Node* n = SearchBST(root, node);
// if right subtree exists
if (n->right != NULL)
return findMinimum(n->right);
// if node does not have a right subtree travel up using parent pointer
Node* p = n->parent;
while (p != NULL && n == p->right) {
n = p;
p = p->parent;
}
return p;
}
/* Driver Code */
int main(){
int size, i, key;
cout<<"Enter size of array: ";
cin>>size;
int arr[size];
cout<<"Enter array elements: ";
for(int i=0;i<size;i++)
cin>>arr[i];
Node* root = nullptr;
for(int i=0;i<size;i++){
key=arr[i];
root = insert(root, key);
}
for(int i=0;i<size;i++){
key=arr[i];
Node* succ = InorderSuccessor(root, key);
if (succ != nullptr)
cout << "The successor of node " << key << " is " << succ->val;
else
cout << "The successor of node " << key << " is NULL." ;
cout << endl;
}
return 0;
}
Java
import java.io.*;
import java.util.*;
// Structure of a BST node
class Node{
int val;
Node left = null, right = null, parent = null;
Node(int val) {
this.val = val;
}
}
class Main{
// Recursive function to insert a key into a BST
public static Node insert(Node root, int key){
// create a new node if the root is null
if (root == null) {
return new Node(key);
}
else if (key < root.val) {
Node temp = insert(root.left, key);
root.left = temp;
temp.parent = root;
}
else {
Node temp = insert(root.right, key);
root.right = temp;
temp.parent = root;
}
return root;
}
// function to locate node whose inorder successor is to be found
public static Node SearchBST (Node root, int key) {
if (root == null || root.val == key) {
return root;
} else if (root.val < key) {
return SearchBST(root.right, key);
} else if (root.val > key) {
return SearchBST(root.left, key);
}
return null;
}
/*Function to find minimum value node in a given BST*/
public static Node findMinimum(Node root){
while (root.left != null) {
root = root.left;
}
return root;
}
/*Function to find an inorder successor*/
public static Node InorderSuccessor(Node root, int node){
Node n = SearchBST(root, node);
// if right subtree exists
if (n.right != null) {
return findMinimum(n.right);
}
// if node does not have a right subtree travel up using parent pointer
Node p = n.parent;
while (p != null && n == p.right) {
n = p;
p = p.parent;
}
return p;
}
/*Driver Code*/
public static void main(String[] args){
int size, i, key;
Scanner sc=new Scanner(System.in);
System.out.print("Enter size of array: ");
size=sc.nextInt();
int[] arr = new int[size];
System.out.print("Enter array elements: ");
for(i=0; i<size; i++)
{arr[i]=sc.nextInt();}
Node root = null;
for(i=0;i<size;i++){
key=arr[i];
root = insert(root, key);
}
for(i=0;i<size;i++){
key=arr[i];
Node succ = InorderSuccessor(root, key);
if (succ != null)
System.out.println("The successor of node " + key + " is "+ succ.val);
else
System.out.println("The successor of node " + key + " is NULL");
}
}
}
Python
# Structure of a BST node
class Node:
def __init__(self, value, left=None, right=None, parent=None):
self.val = value
self.left = left
self.right = right
self.parent= parent
# Recursive function to insert a key into a BST
def insert(root, key):
# create new node if root is none
if root is None:
return Node(key)
elif key < root.val:
temp = insert(root.left, key)
root.left = temp
temp.parent = root
else:
temp = insert(root.right, key)
root.right = temp
temp.parent = root
return root
# function to find minimum value node in a given BST
def findMinimum(root):
while root.left:
root = root.left
return root
#function to locate node whose inorder successor is to be found
def SearchBST (root, key) :
if (root == None or root.val == key) :
return root
elif (root.val < key) :
return SearchBST(root.right, key)
else :
return SearchBST(root.left, key)
# Function to find an inorder successor for a given key using parent pointer
def InorderSuccessor(root, node):
n = SearchBST(root, node)
#if right subtree exists
if (n.right):
return findMinimum(n.right)
# if node does not have a right subtree travel up using parent pointer
p = n.parent
while( p is not None):
if n != p.right :
break
n = p
p = p.parent
return p
#driver code
if __name__ == '__main__':
size=int(input("Enter size of array: "))
arr = list(map (int, input ("Enter array elements: ").split ()))
root = None
for key in arr:
root = insert(root, key)
for key in arr:
succ = InorderSuccessor(root, key)
if succ:
print("The successor of node "+ str(key) +" is "+ str(succ.val) + ".")
else:
print("The successor of node "+ str(key) +" is NULL.")
Output
Enter size of array: 6
Enter array elements: 7 11 3 4 5 15
The successor of node 7 is 11.
The successor of node 11 is 15.
The successor of node 3 is 4.
The successor of node 4 is 5.
The successor of node 5 is 7.
The successor of node 15 is NULL.
Time complexity The time complexity for this approach is O(h), where h is the number of nodes in the Binary Search Tree (or the number of elements in the array).
Space complexity The space complexity for this approach will be O(1) since no extra space is required.
Method 2 (Search from root)
Algorithm
- Step 1 – No parent pointer is involved in this approach.
- Step 2 – Check the right subtree of the input node.
- If the right subtree of the node exists, then the successor (succ) lies in the right subtree. The node with minimum key value in the right subtree is returned.
- If the node does not contain a right subtree a search-like technique is implemented to travel down the tree from the root. Move towards the right if the value of a current node is greater than the root’s data, else move towards the left.
Code Implementation C++
#include <iostream>
using namespace std;
// Structure of a BST node
struct Node{
int val;
Node* left = nullptr;
Node*right = nullptr;
Node() {}
Node(int val): val(val) {}
};
// Recursive function to insert a key into a BST
Node* insert(Node* root, int key){
// create a new node if the root is null
if (root == nullptr)
return new Node(key);
if (key < root->val)
root->left = insert(root->left, key);
else
root->right = insert(root->right, key);
return root;
}
// Function to find minimum value node in a given BST
Node* findMinimum(Node* root){
while (root->left)
root = root->left;
return root;
}
/* Function to find an inorder successor */
Node* InorderSuccessor(Node* root, int node){
Node* succ = NULL;
/*Start from root and search for successor down the tree*/
while (root != NULL){
// if right subtree exist
if (root->val==node && root->right != NULL)
return findMinimum(root->right);
// if node does not have a right subtree
else if (node < root->val){
succ = root;
root = root->left;
}
else if (node > root->val)
root = root->right;
else
break;
}
return succ;
}
/* Driver Code */
int main(){
int size, i, key;
cout<<"Enter size of array: ";
cin>>size;
int arr[size];
cout<<"Enter array elements: ";
for(int i=0;i<size;i++)
cin>>arr[i];
Node* root = nullptr;
for(int i=0;i<size;i++){
key=arr[i];
root = insert(root, key);
}
for(int i=0;i<size;i++){
key=arr[i];
Node* succ = InorderSuccessor(root, key);
if (succ != nullptr)
cout << "The successor of node " << key << " is " << succ->val;
else
cout << "The successor of node " << key << " is NULL." ;
cout << endl;
}
return 0;
}
Java
import java.io.*;
import java.util.*;
// Structure of a BST node
class Node{
int val;
Node left = null, right = null;
Node(int val) {
this.val = val;
}
}
class Main{
// Recursive function to insert a key into a BST
public static Node insert(Node root, int key){
// create a new node if the root is null
if (root == null) {
return new Node(key);
}
// if the given key is less than the root node, recur for the left subtree
if (key < root.val) {
root.left = insert(root.left, key);
}
// if the given key is more than the root node, recur for the right subtree
else {
root.right = insert(root.right, key);
}
return root;
}
/*Function to find minimum value node in a given BST*/
public static Node findMinimum(Node root){
while (root.left != null) {
root = root.left;
}
return root;
}
/*Function to find an inorder successor*/
public static Node InorderSuccessor(Node root, int node){
Node succ = null;
/*Start from root and search for successor down the tree*/
while (root != null){
// if right subtree exist
if (root.val==node && root.right != null)
return findMinimum(root.right);
// if node does not have a right subtree
else if (node < root.val){
succ = root;
root = root.left;
}
else if (node > root.val)
root = root.right;
else
break;
}
return succ;
}
/*Driver Code*/
public static void main(String[] args){
int size, i, key;
Scanner sc=new Scanner(System.in);
System.out.print("Enter size of array: ");
size=sc.nextInt();
int[] arr = new int[size];
System.out.print("Enter array elements: ");
for(i=0; i<size; i++)
{arr[i]=sc.nextInt();}
Node root = null;
for(i=0;i<size;i++){
key=arr[i];
root = insert(root, key);
}
for(i=0;i<size;i++){
key=arr[i];
Node succ = InorderSuccessor(root, key);
if (succ != null)
System.out.println("The successor of node " + key + " is "+ succ.val);
else
System.out.println("The successor of node " + key + " is NULL");
}
}
}
Python
# Structure of a BST node
class Node:
def __init__(self, value, left=None, right=None):
self.val = value
self.left = left
self.right = right
# Recursive function to insert a key into a BST
def insert(root, key):
# create new node if root is none
if root is None:
return Node(key)
if key < root.val:
root.left = insert(root.left, key)
else:
root.right = insert(root.right, key)
return root
# function to find minimum value node in a given BST
def findMinimum(root):
while root.left:
root = root.left
return root
# Function to find an inorder successor for a given key in a BST by traversing from root
def InorderSuccessor(root, node):
succ=Node(None)
#Start from root and search for successor down the tree
while(root):
#if right subtree exists
if (root.val==node and root.right):
return findMinimum(root.right)
# if node does not have a right subtree
elif(root.val<node):
root=root.right
elif(root.val>node):
succ=root
root=root.left
else:
break
return succ
#driver code
if __name__ == '__main__':
size=int(input("Enter size of array: "))
arr = list(map (int, input ("Enter array elements: ").split ()))
root = None
for key in arr:
root = insert(root, key)
for key in arr:
succ = InorderSuccessor(root, key)
if succ:
print("The successor of node "+ str(key) +" is "+ str(succ.val) + ".")
else:
print("The successor of node "+ str(key) +" is NULL.")
Output
Enter size of array: 6
Enter array elements: 7 11 3 4 5 15
The successor of node 7 is 11.
The successor of node 11 is 15.
The successor of node 3 is 4.
The successor of node 4 is 5.
The successor of node 5 is 7.
The successor of node 15 is None.
Time Complexity The time complexity for this approach is O(h), where h is the number of nodes in the Binary Search Tree (or the number of elements in the array).
Space Complexity The space complexity for this approach will be O(1) since no extra space is required.
Method 3 (Recursive Approach)
Algorithm
- Step 1 – At the initial step, the given node is searched in the tree and the successor is updated to the current node before visiting its left subtree.
- Step 2 – If a node with the desired value is found in the BST, the least value node in its right subtree is returned.
- Step 3 – In case, the node does not have a right subtree, the inorder successor is found in one of its ancestors using recursion.
Code Implementation C++
#include <iostream>
using namespace std;
// Structure of a BST node
struct Node{
int val;
Node* left = nullptr;
Node*right = nullptr;
Node() {}
Node(int val): val(val) {}
};
// Recursive function to insert a key into a BST
Node* insert(Node* root, int key){
// create a new node if the root is null
if (root == nullptr)
return new Node(key);
if (key < root->val)
root->left = insert(root->left, key);
else
root->right = insert(root->right, key);
return root;
}
// Function to find minimum value node in a given BST
Node* findMinimum(Node* root){
while (root->left)
root = root->left;
return root;
}
// Recursive function to find an inorder successor
Node* InorderSuccessor(Node* root, Node* succ, int key){
// base case
if (root == nullptr)
return succ;
// if a node with the desired value is found, the successor is the minimum value
if (root->val == key){
if (root->right != nullptr)
return findMinimum(root->right);
}
// if the given key is less than the root node, consider the left subtree
else if (key < root->val){
succ = root;
return InorderSuccessor(root->left, succ, key);
}
//consider for the right subtree
else
return InorderSuccessor(root->right, succ, key);
return succ;
}
/* Driver Code */
int main(){
int size, i, key;
cout<<"Enter size of array: ";
cin>>size;
int arr[size];
cout<<"Enter array elements: ";
for(int i=0;i<size;i++)
cin>>arr[i];
Node* root = nullptr;
for(int i=0;i<size;i++){
key=arr[i];
root = insert(root, key);
}
for(int i=0;i<size;i++){
key=arr[i];
Node* succ = InorderSuccessor(root, nullptr, key);
if (succ != nullptr)
cout << "The successor of node " << key << " is " << succ->val;
else
cout << "The successor of node " << key << " is NULL." ;
cout << endl;
}
return 0;
}
Java
import java.io.*;
import java.util.*;
// Structure of a BST node
class Node{
int val;
Node left = null, right = null;
Node(int val) {
this.val = val;
}
}
class Main{
// Recursive function to insert a key into a BST
public static Node insert(Node root, int key){
// create a new node if the root is null
if (root == null) {
return new Node(key);
}
// if the given key is less than the root node, recur for the left subtree
if (key < root.val) {
root.left = insert(root.left, key);
}
// if the given key is more than the root node, recur for the right subtree
else {
root.right = insert(root.right, key);
}
return root;
}
// Function to find minimum value node in a given BST
public static Node findMinimum(Node root){
while (root.left != null) {
root = root.left;
}
return root;
}
// Recursive function to find an inorder successor
public static Node InorderSuccessor(Node root, Node succ, int key){
// base case
if (root == null) {
return succ;
}
// if a node with the desired value is found, the successor is the minimum
if (root.val == key){
if (root.right != null) {
return findMinimum(root.right);
}
}
// if the given key is less than the root node, consider the left subtree
else if (key < root.val){
succ = root;
return InorderSuccessor(root.left, succ, key);
}
// if the given key is more than the root node, consider the right subtree
else {
return InorderSuccessor(root.right, succ, key);
}
return succ;
}
/*Driver Code*/
public static void main(String[] args){
int size, i, key;
Scanner sc=new Scanner(System.in);
System.out.print("Enter size of array: ");
size=sc.nextInt();
int[] arr = new int[size];
System.out.print("Enter array elements: ");
for(i=0; i<size; i++)
{arr[i]=sc.nextInt();}
Node root = null;
for(i=0;i<size;i++){
key=arr[i];
root = insert(root, key);
}
for(i=0;i<size;i++){
key=arr[i];
Node succ = InorderSuccessor(root, null, key);
if (succ != null)
System.out.println("The successor of node " + key + " is "+ succ.val);
else
System.out.println("The successor of node " + key + " is NULL");
}
}
}
Python
# Structure of a BST node
class Node:
def __init__(self, value, left=None, right=None):
self.val = value
self.left = left
self.right = right
# Recursive function to insert a key into a BST
def insert(root, key):
# create new node if root is none
if root is None:
return Node(key)
if key < root.val:
root.left = insert(root.left, key)
else:
root.right = insert(root.right, key)
return root
# function to find minimum value node in a given BST
def findMinimum(root):
while root.left:
root = root.left
return root
# Recursive function to find an inorder successor for a given key in a BST
def InorderSuccessor(root, succ, key):
if root is None:
return succ
# if a node with the desired value is found, the successor is the minimum value
# node in its right subtree
if root.val == key:
if root.right:
return findMinimum(root.right)
# consider for the left subtree if the given key is less than the root node,
elif key < root.val:
succ = root
return InorderSuccessor(root.left, succ, key)
# else consider right subtree
else:
return InorderSuccessor(root.right, succ, key)
return succ
#driver code
if __name__ == '__main__':
size=int(input("Enter size of array: "))
arr = list(map (int, input ("Enter array elements: ").split ()))
root = None
for key in arr:
root = insert(root, key)
for key in arr:
succ = InorderSuccessor(root, None, key)
if succ:
print("The successor of node "+ str(key) +" is "+ str(succ.val) + ".")
else:
print("The successor of node "+ str(key) +" is NULL.")
Output
Enter size of array: 6
Enter array elements: 7 11 3 4 5 15
The successor of node 7 is 11.
The successor of node 11 is 15.
The successor of node 3 is 4.
The successor of node 4 is 5.
The successor of node 5 is 7.
The successor of node 15 is NULL.
Time complexity The time complexity for the recursive approach is O(h), where h is the number of nodes in the Binary Search Tree (or the number of elements in the array). In the worst case, the entire tree of height (h) needs to be traversed.
Space complexity The space complexity for this approach will be O(1) since no extra space is required.
Method 4 (Iterative Approach)
Algorithm
- Step 1 – At the initial step, the given node is searched in the tree and the successor is updated to the current node before visiting its left subtree.
- Step 2 – If a node with the desired value is found in the BST, the least value node in its right subtree is returned.
- Step 3 – In case, the node does not have a right subtree, the inorder successor is found in one of its ancestors using iteration.
Code Implementation C++
#include <iostream>
using namespace std;
// Structure of a BST node
struct Node{
int val;
Node* left = nullptr;
Node*right = nullptr;
Node() {}
Node(int val): val(val) {}
};
// Recursive function to insert a key into a BST
Node* insert(Node* root, int key){
// create a new node if the root is null
if (root == nullptr)
return new Node(key);
if (key < root->val)
root->left = insert(root->left, key);
else
root->right = insert(root->right, key);
return root;
}
/* Function to find minimum value node in a given BST */
Node* findMinimum(Node* root){
while (root->left)
root = root->left;
return root;
}
/* Iterative function to find an inorder successor for a given key in a BST */
Node* InorderSuccessor(Node* root, Node* succ, int key){
// base case
if (root == nullptr)
return nullptr;
succ = nullptr;
while (true){
/* visit the left subtree if the key is less than the root node value */
if (key < root->val){
succ = root;
root = root->left;
}
/* visit the right subtree if the key is more than the root node value */
else if (key > root->val)
root = root->right;
/* if a node with the desired value is found, the successor is the minimum value node in its right subtree*/
else {
if (root->right)
succ = findMinimum(root->right);
break;
}
/* if the key doesn't exist in the binary tree, return next greater node */
if (!root)
return succ;
}
// return successor
return succ;
}
/* Driver Code */
int main(){
int size, i, key;
cout<<"Enter size of array: ";
cin>>size;
int arr[size];
cout<<"Enter array elements: ";
for(int i=0;i<size;i++)
cin>>arr[i];
Node* root = nullptr;
for(int i=0;i<size;i++){
key=arr[i];
root = insert(root, key);
}
for(int i=0;i<size;i++){
key=arr[i];
Node* succ = InorderSuccessor(root, nullptr, key);
if (succ != nullptr)
cout << "The successor of node " << key << " is " << succ->val;
else
cout << "The successor of node " << key << " is NULL." ;
cout << endl;
}
return 0;
}
Java
import java.io.*;
import java.util.*;
// Structure of a BST node
class Node{
int val;
Node left = null, right = null;
Node(int val) {
this.val = val;
}
}
class Main{
// Recursive function to insert a key into a BST
public static Node insert(Node root, int key){
// create a new node if the root is null
if (root == null) {
return new Node(key);
}
// if the given key is less than the root node, recur for the left subtree
if (key < root.val) {
root.left = insert(root.left, key);
}
// if the given key is more than the root node, recur for the right subtree
else {
root.right = insert(root.right, key);
}
return root;
}
// Function to find minimum value node in a given BST
public static Node findMinimum(Node root){
while (root.left != null) {
root = root.left;
}
return root;
}
/* Iterative function to find an inorder successor for a given key in a BST */
public static Node InorderSuccessor(Node root, Node succ, int key){
// base case
if (root == null) {
return succ;
}
succ = null;
while (true){
/* visit the left subtree if the key is less than the root node value */
if (key < root.val){
// update successor to the current node before visiting left subtree
succ = root;
root = root.left;
}
/* visit the right subtree if the key is more than the root node value */
else if (key > root.val) {
root = root.right;
}
/* if a node with the desired value is found, the successor is the minimum value node in its right subtree*/
else {
if (root.right != null) {
succ = findMinimum(root.right);
}
break;
}
// if the key doesn't exist in the binary tree, return next greater node
if (root == null) {
return succ;
}
}
// return successor
return succ;
}
/*Driver Code*/
public static void main(String[] args){
int size, i, key;
Scanner sc=new Scanner(System.in);
System.out.print("Enter size of array: ");
size=sc.nextInt();
int[] arr = new int[size];
System.out.print("Enter array elements: ");
for(i=0; i<size; i++)
{arr[i]=sc.nextInt();}
Node root = null;
for(i=0;i<size;i++){
key=arr[i];
root = insert(root, key);
}
for(i=0;i<size;i++){
key=arr[i];
Node succ = InorderSuccessor(root, null, key);
if (succ != null)
System.out.println("The successor of node " + key + " is "+ succ.val);
else
System.out.println("The successor of node " + key + " is NULL");
}
}
}
Python
# Structre of a BST node
class Node:
def __init__(self, value, left=None, right=None):
self.val = value
self.left = left
self.right = right
# Fnction to insert a key into a BST
def insert(root, key):
# create new node if root is none
if root is None:
return Node(key)
if key < root.val:
root.left = insert(root.left, key)
else:
root.right = insert(root.right, key)
return root
# function to find minimum value node in a given BST
def findMinimum(root):
while root.left:
root = root.left
return root
# Iterative function to find an inorder successor for a given key in a BST
def InorderSuccessor(root, succ, key):
if root is None:
return None
succ = None
while True:
# visit the left subtree if the key is less than the root node value
if key < root.val:
# update successor to the current node before visiting
succ = root
root = root.left # left subtree
# visit the right subtree if the key is more than the root node value
elif key > root.val:
root = root.right
# if a node with the desired value is found, the successor is the minimum value node in its right subtree
else:
if root.right:
succ = findMinimum(root.right)
break
# if the key doesn't exist in the binary tree, return next greater node
if root is None:
return succ
# return successor
return succ
#driver code
if __name__ == '__main__':
size=int(input("Enter size of array: "))
arr = list(map (int, input ("Enter array elements: ").split ()))
root = None
for key in arr:
root = insert(root, key)
for key in arr:
succ = InorderSuccessor(root, None, key)
if succ:
print("The successor of node "+ str(key) +" is "+ str(succ.val) + ".")
else:
print("The successor of node "+ str(key) +" is NULL.")
Output
Enter size of array: 6
Enter array elements: 7 11 3 4 5 15
The successor of node 7 is 11
The successor of node 11 is 15
The successor of node 3 is 4
The successor of node 4 is 5
The successor of node 5 is 7
The successor of node 15 is NULL.
Time Complexity The time complexity for the iterative approach is O(h), where h is the number of nodes in the Binary Search Tree (or the number of elements in the array). In the worst case, the entire tree of height (h) needs to be traversed.
Space Complexity The space complexity for this approach will be O(1), since no extra space is required.
Learn more
Conclusion
- Inorder traversal of a BST gives us elements in ascending order sorted manner.
- The Inorder Successor of a given key in the Binary Search Tree is the node that appears just after the given key node in the inorder traversal of the BST.
- Approach 1 – Using a parent pointer the tree is traversed to find the inorder successor.
- Time Complexity : O(h)
- Space Complexity (1)
- Approach 2 – This approach involves searching from the root of the BST without using a parent pointer.
- Time Complexity : O(h)
- Space Complexity (1)
- Approach 3 – Carrying out inorder transversal of BST using recursion, as this produces a sorted sequence.
- Time Complexity : O(h)
- Space Complexity (1)
- Approach 4 – Carrying out inorder transversal of BST using iteration, as this produces a sorted sequence.
- Time Complexity : O(h)
- Space Complexity (1)